Đây là bài thứ 1 of 3 trong series Các dạng toán và phương pháp giải Toán lớp 6
Và phép trừ, phép chia, lũy thừa với số mũ tự nhiên, thứ tự thực hiện các phép tính…
Bài 1: Tập hợp. Phần tử của tập hợp
Dạng 1: Viết một tập hợp cho trước
Phương pháp giải
Dùng một chữ cái in hoa và dấu ngoặc nhọn, ta có thể viết một tập hợp theo hai cách:
– Liệt kê các phần tử của nó.
– Chỉ ra tính chất đặc trưng cho các phần tử của nó
Dạng 2: Sử dụng các kí hiệu ∈ và ∉
Phương pháp giải
Dạng 3: Minh họa một tập hợp cho trước bằng hình vẽ
Phương pháp giải
Sử dụng biểu đồ ven. Đó là một đường cong khép kín, không tự cắt, mỗi phần tử của tập hợp được biểu diễn bởi một điểm ở bên trong đường cong đó.
Bài 2: Tập hợp các số tự nhiên
Dạng 1: Tìm số liền sau, số liền trước của một số tự nhiên cho trước
Phương pháp giải
– Để tìm số liền sau của số tự nhiên a, ta tính a+1
– Để tìm số liền trước của số tự nhiên a khác 0, ta tính a-1
Chú ý: – Số 0 không có số liền trước.
– Hai số tự nhiên liên tiếp thì hơn kém nhau 1 đơn vị.
Dạng 2: Tìm các số tự nhiên thỏa mãn điều kiện cho trước
Phương pháp giải
Liệt kê tất cả các số tự nhiên thỏa mãn đồng thời các điều kiện đã cho
Dạng 3: Biểu diễn trên tia số các số tự nhiên thỏa mãn điều kiện cho trước
Phương pháp giải
– Liệt kê các số tự nhiên thỏa mãn đồng thời các điều kiện đã cho
– Biểu diễn các số vừa liệt kê trên tia số
Bài 3: Ghi số tự nhiên
Dạng 1: Ghi các số tự nhiên
Phương pháp giải
– Sử dụng cách tách số tự nhiên thành từng lớp để ghi.
-Chú ý phân biệt: Số với chữ số, số chục với chữ số hàng chục, số trăm với chữ số hàng trăm…
Dạng 2: Viết tất cả các số có n chữ số từ n chữ số cho trước
Phương pháp giải
Giả sử từ ba chữ số a, b, c khác 0, ta viết các số có ba chữ số như sau:
– Làm tính nhân từ phải sang trái, căn cứ vào những hiểu biết về tính chất
của số tự nhiên và của phép tính, suy luận từng bước để tìm ra những số chưa biết.
Dạng 6: So sánh hai tổng hoặc hai tích mà không tính cụ thể giá trị của chúng
Phương pháp giải
Nhận xét, phát hiện và sử dụng các đặc điểm của các số hạng hoặc các thừa số trong tổng hoặc tích.
Từ đó dựa vào các tính chất của phép cộng và phép nhân để rút ra kết luận.
Dạng 7: Tìm số tự nhiên có nhiều chữ số khi biết điều kiện xác định các chữ số trong số đó
Phương pháp giải
Dựa vào điều kiện xác định các chữ số trong số tự nhiên cần tìm để tìm từng chữ số có mặt trong số tự nhiên đó.
Bài 6: Phép trừ và phép chia
Dạng 1: Thực hành phép trừ và phép chia
Phương pháp giải
– Có thể trừ theo “hàng ngang” hoặc viết số trừ dưới số bị trừ sao cho các chữ số cùng hàng thì thẳng cột với nhau rồi trừ từ phải sang trái.
– Đặt phép chia và thử lại kết quả bằng phép nhân.
– Sử dụng máy tính bỏ túi (đối với những bài được phép dùng).
Dạng 2: Áp dụng tính chất các phép tính để tính nhanh
Phương pháp giải
Áp dụng một số tính chất sau đây:
– Tổng của hai số không đổi nếu ta thêm vào ở số hạng này và bớt đi ở số hạng kia cùng một số đơn vị.
Ví dụ: 99 + 48 = (99+1)-( 48-1) = 100+ 47 = 147.
– Hiệu của hai số không đổi nếu ta thêm vào một số bị trừ và số trừ cùng một số đơn vị.
Ví dụ: 316-97 =(316+3) – (97+3) = 319-100= 219
– Tích của hai só không đổi nếu ta nhân thừa số này và chia thừa số kia cho cùng một số
Ví dụ: 25.12 = (25.4).(12:4) = 100.3 =300
– Thương của hai số không đổi nếu ta nhân cả số bị chia và số chia với cùng một số.
Ví dụ: 1200: 50 =( 1200.2) : (50.2) =2400:100 =24.
– Chia một tổng cho một số (a+b) : c = a: c + b:c (trường hợp chia hết).
Ví dụ: 276:23 = (230 + 46) : 23 = 230:23 + 46:23 = 10 + 2 =12.
Dạng 3: Tìm số chưa biết trong một đẳng thức
Phương pháp giải
Dạng 4: Bài tập về phép chia có dư
Phương pháp giải
Sử dụng định nghĩa của phép chia có dư và công thức:
a = b.q + r (0< r < b)
Từ công thức trên suy ra : b = (a – r) : q; q = (a – r) : b; r = a –b.q.
Dạng 5: Tìm những chữ số chưa biết trong phép trừ và phép chia
Phương pháp giải
– Đối với phép trừ, tính lần lượt theo cột từ phải sang trái, chú ý những trường hợp có “nhớ”.
– Đối với phép chia, đặt tính và lần lượt thực hiện phép chia.
Bài 7: Lũy thừa với số mũ tự nhiên
Nhân hai lũy thừa cùng cơ số.
Dạng 1: Viết gọn một tích bằng cách dùng lũy thừa
Phương pháp giải
Bài 9: Thứ tự thực hiện các phép tính
Dạng 1: Thực hiện các phép tính theo thứ tự đã quy định
Phương pháp giải
Thực hiện theo đúng thứ tự quy định đối với biểu thức có dấu ngoặc và biểu thức không có dấu ngoặc
Dạng 2: Tìm số chưa biết trong đẳng thức hoặc trong một sơ đồ
Phương pháp giải
Dạng 3: So sánh giá trị hai biểu thức đại số
Phương pháp giải
Tính riêng giá trị của mỗi biểu thức rồi so sánh hai kết quả tìm được.
Bài 10: Tính chất chia hết của một tổng
Dạng 1: Xét tính chia hết của một tổng hoặc một hiệu
Phương pháp giải
Áp dụng tính chất 1 và tính chất 2 về sự chia hết của một tổng, một hiệu.
Dạng 2: Tìm điều kiện của một số hạng để tổng hoặc hiệu chia hết cho một số nào đó
Phương pháp giải
Áp dụng tính chất 1 và tính chất 2 để tìm điều kiện của số hạng chưa biết.
Dạng 3: Xét tính chia hết của một tích
Phương pháp giải
Áp dụng tính chất: Nếu trong một tích các số tự nhiên có một thừa số chia hết cho một số nào đó thì tích cũng chia hết cho số đó.
Bài 11: Dấu hiệu chia hết cho 2 và cho 5
Dạng 1: Nhận biết các số chia hết cho 2 và cho 5
Phương pháp giải
Dạng 2: Viết các số chia hết cho 2, cho 5 từ các số hoặc các chữ số cho trước
Phương pháp giải
Dạng 3: Toán có liên quan đến số dư trong phép chia một số tự nhiên cho 2, cho 5
Phương pháp giải
* Chú ý rằng:
– Số dư trong phép chia cho 2 chỉ có thể là 0 hoặc 1.
– Số dư trong phép chia cho 5 chỉ có thể là 0, hoặc1,hoặc 2, hoặc 3, hoặc 4.
Dạng 4: Tìm tập hợp các số tự nhiên chia hết cho 2, cho 5 trong một khoảng cho trước.
Phương pháp giải
Ta liệt kê tất cả các số chia hết cho 2, cho 5 (căn cứ vào dấu hiệu chia hết ) trong khoảng đã cho.
Bài 12: Dấu hiệu chia hết cho 3, cho 9
Dạng 1: Nhận biết các số chia hết cho 3, cho 9
Phương pháp giải
* Chú ý:
Dạng 2: Viết các số chia hết cho 3, cho 9 từ các số hoặc các chữ số cho trước.
Phương pháp giải
Sử dụng các dấu hiệu chia hết cho 3, cho 9 (có thể cả dấu hiệu chia hết cho 2, cho 5)
Dạng 3: Toán có liên quan đến số dư trong phép chia một số tự nhiên cho 3, cho 9
Phương pháp giải
-Sử dụng tính chất: một số có tổng các chữ số chia hết cho 9 ( cho 3 ) dư m thì số đó chia hết cho 9 (cho 3 ) cũng dư m
Ví dụ : 235 có tổng các chữ số bằng 2+3+4+5 =14. Số 14 chia cho 9 dư 5, chia cho 3 dư 2. Do đó số 2345 chia cho 9 dư 5, chia cho 3 dư 2.
Dạng 4: Tìm tập hợp các số tự nhiên chia hết cho 3, cho 9 trong một khoảng cho trước
Phương pháp giải
-Ta liệt kê tất cả các số thuộc khoảng đã cho mà có tổng các chữ số chia hết cho 3, cho 9
Bài 13: Ước và bội
Dạng 1: Tìm và viết tập hợp các ước, tập hợp các bội của một số cho trước
Phương pháp giải
– Để tìm ước của một số, ta chia số đó lần lượt cho 1, 2, 3…
– Để tìm bội của một số khác 0, ta nhân số đó lần lượt với 0, 1, 2, 3…
Dạng 2: Viết tất cả các số là bội hoặc ước của một số cho trước và thỏa mãn điều kiện cho trước
Phương pháp giải
Tìm trong các số thỏa mãn điều kiện cho trước những số là bội hoặc ước của số đã cho.
Dạng 3: Bài toán đưa về việc tìm ước hoặc bội của một số cho trước
Phương pháp giải
Bài 14: Số nguyên tố. Hợp số
Bảng số nguyên tố.
Dạng 1: Nhận biết số nguyên tố, hợp số
Phương pháp giải
Dạng 2: Viết số nguyên tố hoặc hợp số từ những số cho trước
Phương pháp giải
Dạng 3: Chứng minh một số là số nguyên tố hay hợp số.
Phương pháp giải
Bài 15 : Phân tích một số ra thừa số nguyên tố
Dạng 1: Phân tích các số cho trước ra thừa số nguyên tố
Phương pháp giải:
Thường có hai cách phân tích một số tự nhiên n (n >1) ra thừa số nguyên tố.
Cách 1 (phân tích theo cột dọc ): Chia số n cho một số nguyên tố (xét từ nhỏ đến lớn ), rồi chia thương tìm được cho một số nguyên tố (cũng xét từ nhỏ đến lớn), cứ tiếp tục như vậy cho đến khi thương bằng 1.
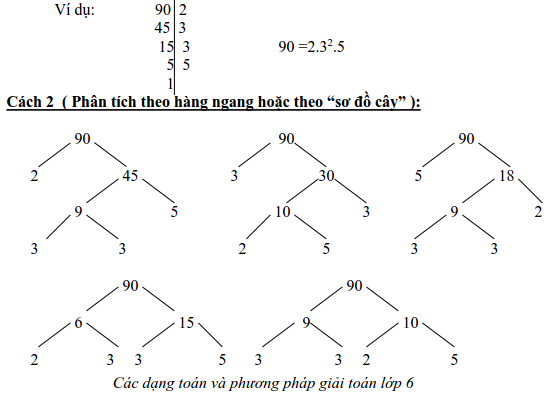
Bài 18: Bội chung nhỏ nhất
Dạng 1: Tìm bội chung nhỏ nhất của các số cho trước
Phương pháp giải
Dạng 2: Bài toán đưa về việc tìm BCNN của hai hay nhiều số.
Phương pháp giải
Phân tích đề bài, suy luận để đưa về việc tìm BCNN của hai hay nhiều số.
Dạng 3: Bài toán đưa về việc tìm bội chung của hai hay nhiều số thỏa mãn điều kiện cho trước
Phương pháp giải