Đó là các phương pháp quy nạp, khử liên tiếp. Các em xem tiếp lý thuyết và bài tập áp dụng có lời giải dưới đây.
– Đối với 1 số trường hợp khi tính tổng hữu hạn:
Sn = a1 + a2 + . . . +an (*)
khi mà ta có thể biết được kết quả (đề bài toán cho ta biết kết quả hoặc ta dự đoán được kết quả), thì ta sử dụng phương pháp quy nạp này để chứng minh.
* Ví dụ: Tính tổng Sn = 1 +3 +5 +. . . +(2n -1)
° Hướng dẫn: (sử dụng phương pháp quy nạp)
– Đầu tiên, ta thử với n = 1, ta có: S1 = (2.1 – 1) = 1
Thử với n = 2, ta có: S2 = (2.1 – 1) (2.2 – 1) = 1 +3 = 4 = 22
Thử với n= 3, ta có: S3 = (2.1 – 1) (2.2 – 1) (2.3 – 1)= 1 +3 +5 = 9 = 32
… … …
– Ta dự đoán: Sn = 1 +3 +5 . . . (2n -1) = n2
• Phương pháp quy nạp: Sn = 1 +3 +5 . . . (2n -1) = n2 (*)
Với n = 1; S1 = 1 (đúng)
Giả sử đúng với n = k (k≠1), tức là:
Sk =1 +3 +5 . . . (2k -1) = k2 (1)
Ta cần chứng minh (*) đúng với n = k +1, tức là:
Sk +1 = 1 +3 +5 . . . (2k-1) (2k +1) = (k +1)2
Vì ta đã giải sử Sk đúng nên ta đã có (1), từ đây ta biến đổi để xuất hiện (2), (1) còn được gọi là giải thiết quy nạp.
1 +3 +5 . . . +(2k -1) = k2
1 +3 +5 . . .+ (2k-1) + (2k +1) = k2 (2k +1) (cộng 2k+ 1 vào 2 vế).
Từ đó ⇒ 1 +3 +5 . . .+ (2k-1) + (2k +1) = k2 + 2k +1 = (k +1)2
• Tương tự như vậy, ta có thể chứng minh các kết quả sau bằng phương pháp quy nạp toán học:
1) ![]()
2) ![]()
3) ![]()
4) ![]()
– Giả sử cần tính tổng: Sn = a1 a2 . . . an (*) mà ta có thể biểu diễn ai, i =1,2,3,…,n qua hiệu của 2 số hạng liên tiếp của 1 dãy khác, cụ thể như sau:
a1 = b1 – b2
a2 = b2 – b3
… … …
an = bn – bn +1
⇒ Khi đó ta có: Sn = (b1 – b2) (b2 – b3) … (bn – bn +1) = b1 – bn +1
* Ví dụ 1: Tính tổng:
![]()
° Hướng dẫn: – Ta có:
![]()
![]()
![]() …;
…; ![]()
⇒![]()
![]()
• Dạng tổng quát:
![]()
![]()
* Ví dụ 2: Tính tổng:
![]()
° Hướng dẫn: – Ta có:
![]()
![]() ;…;
;…; ![]()
![]()
![]()
![]()
![]()
* Ví dụ 3: Tính tổng:
![]()
° Hướng dẫn: – Ta có:
![]()
![]()
![]()
• Dạng toán này vận dựng 2 phương pháp giới thiệu ở trên
* Ví dụ 1: Tính tổng: S = 1+2 +22 + . . . +2100 (*)
° Hướng dẫn:
* Cách 1: Ta viết lại S như sau:
S = 1+ 2(1 +2 +22 + . . .+ 299)
S = 1 + 2(1 + 2 + 22 + . . .+ 299 + 2100 – 2100)
⇒ S = 1 + 2(S – 2100) = 1+2S – 2101
⇒ S = 2101 – 1
* Cách 2: Nhân 2 vế với 2, ta được:
2S = 2(1 +2 +22 + . . . 2100)
⇔ 2S = 2 +22 + 23 + . . .+ 2101 (**)
– Lấy (**) trừ đi (*) ta được:
2S – S = (2 + 22 + 23 + . . . +2101) – (1 +2 +22 +. . . +2100)
⇔ S = 2101 – 1.
• Tổng quát cho dạng toán này như sau:
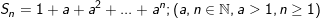
Ta nhân cả 2 vế của Sn với a. Rồi TRỪ vế với vế ta được: ![]()
* Ví dụ 2: Tính:
S = 1 – 2 + 22 – 23 + 24 – . . . – 299 + 2100
° Hướng dẫn:– Ta có:
2S = 2(1 – 2 +22 – 23 + 24 – . . . – 299 + 2100)
⇔ 2S = 2 – 22 + 23 – 24 + 25 – . . . – 2100 + 2101
⇔ 2S S = (2 – 22 + 23 – 24 + 25 – . . . – 2100 + 2101) (1 – 2 + 22 – 23 + 24 – . . . – 299 + 2100)
⇔ 3S = 2101 + 1.
![]()
• Tổng quát cho dạng toán này như sau:
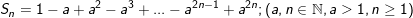
Ta nhân cả 2 vế của Sn với a. Rồi CỘNG vế với vế ta được: ![]()
* Ví dụ 3: Tính tổng:
S = 1+32 + 34 + . . .+ 398 + 3100 (*)
° Hướng dẫn:
– Với bài toán này, mục tiêu là nhân 2 vế của S với một số nào đó mà khi trừ vế với về thì ta được các số khử (triệu tiêu) liên tiếp.
– Đối với bài này, ta thấy số mũ của 2 số liên tiếp cách nhau 2 đơn vị nên ta nhân hai vế với 32 rồi áp dụng phương pháp khử liên tiếp.
S = 1+32 + 34 + . . .+ 398 + 3100
⇔ 32.S = 32(1 +32 + 34 + . . . +398 + 3100)
⇔ 9S= 32 + 34 + . . .+ 3100 + 3102 (**)
– Ta Trừ vế với vế của (**) cho (*) được:
9S-S= (32 + 34 + . . . 3100 + 3102) – (1+32 +34 + . . . +398 + 3100)
⇔ 8S = 3102 – 1
![]()
• Tổng quát cho dạng toán này như sau:
![]()
Ta nhân cả 2 vế của Sn với ad . Rồi TRỪ vế với vế ta được:
![]()
* Ví dụ 4: Tính:
S = 1 – 23 + 26 – 29 . . . +296 – 299 (*)
° Hướng dẫn:
– Lũy thừa các số liên tiếp cách nhau 3 đơn vị, nhân 2 vế với 23 ta được:
23.S = 23.(1 – 23 + 26 – 29 + . . .+ 296 – 299)
⇒ 8S = 23 – 26 + 29 – 212 + . . . +299 – 2102 (**)
– Ta CỘNG vế với vế (**) với (*) được:
8S S = (23 – 26 + 29 – 212 + . . . +299 – 2102) (1 – 23 + 26 – 29 + . . .+ 296 – 299)
⇔ 9S = 1 – 2102 ![]()
• Tổng quát cho dạng toán này như sau:
![]()
Ta nhân cả 2 vế của Sn với ad . Rồi CỘNG vế với vế ta được:
![]()
• Đối với dạng này ở bậc học cao hơn như THPT các em sẽ có công thức tính theo cấp số cộng hoặc cấp số nhân, còn với lớp 6 các em dựa vào cơ sở lý thuyết sau:
– Để đếm được số hạng cảu 1 dãy số mà 2 số hạng liên tiếp cách đều nhau 1 số đơn vị ta dùng công thức:
Số số hạng = [(số cuối – số đầu):(khoảng cách)] 1
– Để tính Tổng các số hạng của một dãy mà 2 số hạng liên tiếp cách đều nhau 1 số đơn vị ta dùng công thức:
Tổng = [(số đầu số cuối).(số số hạng)]:2
* Ví dụ 1: Tính tổng: S = 1+3+5 +7 +… +39
° Hướng dẫn:
– Số số hạng của S là: (39-1):2+1 = 19+1 = 20.
S = [20.(39+1)]:2 = 10.40 = 400.
* Ví dụ 2: Tính tổng: S = 2+5+8+…+59
° Hướng dẫn:
– Số số hạng của S là:(59-2):3+1 = 19+1 = 20.
S = [20.(59+2)]:2 = 10.61 = 610.
• Ký hiệu: ![]()
• Tính chất:
![]()
![]()
* Ví dụ: Tính tổng: Sn = 1.2+2.3 +3.4 … n(n+1)
° Hướng dẫn:
– Ta có: ![]()
– Mặt khác, lại có:
![]() (theo PP quy nạp ở mục I).
(theo PP quy nạp ở mục I).
![]() (theo PP quy nạp ở mục I)
(theo PP quy nạp ở mục I)
![]()
Bài tập 1: Tính tổng: S = 3 8 13 18 … 228
Bài tập 2: Tính các tổng sau:
a) S = 6 +62 + 63 + … +699 + 6100
b) S = 5 +11 +17 … 95 +101
c) ![]()
d) ![]()
Bài tập 3: Chứng minh
a) 1.4 +4.7 +7.10 … (3n-2)(3n+1) = n(n+1)2
b) ![]()