
Kiến thức cần nhớ:

Ví dụ 21. Cho phương trình:
![]()
a) Tìm các giá trị của m để phương trình (1) có hai nghiệm phân biệt.
b) Giải phương trình (1) với m = 5.
Giải
a) Điều kiện để phương trình (1) có hai nghiệm phân biệt là:

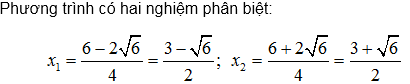
Ví dụ 22. Cho phương trình:
![]()
a) Giải phương trình (1) với m = 1.
b) Tìm giá trị của m để phương trình (1) có nghiệm.
Giải
a) Với m = 1, phương trình (1) có dạng:

BÀI TẬP
133. Giải các phương trình:
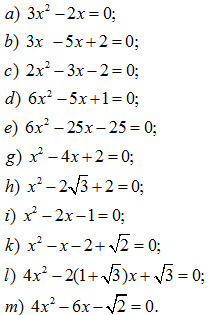
134.
Cho phương trình 2$latex x^{2} $ + 8x + k = 0 có một trong các nghiệm bằng 3. Xác định số k và tìm nghiệm còn lại.
135.
Cho phương trình 6$latex x^{2} $ – 25x – ($latex m^{2} $ + 16) = 0 (m là tham số). Biết một trong các nghiệm của phương trình bằng 5. Tìm tham số m và tìm nghiệm còn lại của phương trình.
136.
Tìm giá trị của m để phương trình sau có nghiệm kép :
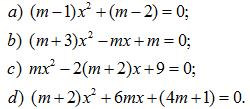
137.
Tìm giá trị của m để phương trình sau có hai nghiệm phân biệt:
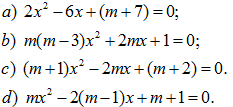
138.
Tìm giá trị của m để phương trình sau vô nghiệm :
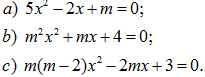
139.
Tìm giá trị của m để phương trình sau có nghiệm :
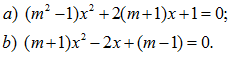
140.
Cho phương trình a$latex x^{2} $ + bx + c = 0. Các khẳng định sau có đúng không?
a) Nếu ac < 0 thì phương trình có hai nghiệm phân biệt.
b) Nếu ac ≤ 0 thì phương trình có nghiệm.
141.
Chứng minh rằng các phương trình sau có nghiệm với mọi giá trị của a :
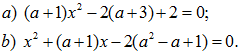
142.
Chứng minh rằng các phương trình sau có nghiệm với mọi giá trị của a, b, c :
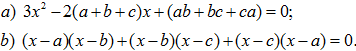
143.
Biện luận số nghiệm của phương trình theo m :
![]()
144.
Giải các phương trình (m là tham số) :
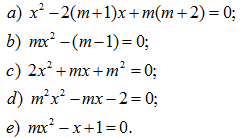
145*.
Cho các phương trình:
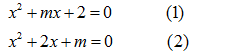
Xác định m, để hai phương trình có nghiệm chung. Tìm nghiệm chung đó.