Chuyên đề hệ phương trình bậc nhất hai ẩn số

MỤC TIÊU: Học sinh nắm được

– Khái niệm hệ phương trình bậc nhất hai ẩn và Cách giải

– Một số dạng toán về hệ phương trình bậc nhất hai ẩn

NỘI DUNG:

KIẾN THỨC CẦN GHI NHỚ

A.1 Hệ hai phương trình bậc nhất hai ẩn

a. Phương trình bậc nhất hai ẩn

• Phương trình bậc nhất hai ẩn: ax + by = c với a, b, c  R (a² + b² ≠ 0)
• Tập nghiệm của phương trình bậc nhất hai ẩn:

Phương trình bậc nhất hai ẩn ax + by = c luôn luôn có vô số nghiệm. Tập nghiệm của nó được biểu diễn bởi đường thẳng (d):  ax + by = c

• Nếu a ≠ 0, b ≠ 0 thì đường thẳng (d) là đồ thị hàm số $ y=-\frac{a}{b}x+\frac{c}{b}$
• Nếu a ≠ 0, b = 0 thì phương trình trở thành ax = c hay x = c/a và đường thẳng (d) song song hoặc trùng với trục tung
• Nếu a = 0, b ≠ 0 thì phương trình trở thành by = c hay y = c/b và đường thẳng (d) song song hoặc trùng với trục hoành

b. Hệ hai phương trình bậc nhất hai ẩn

• Hệ hai phương trình bậc nhất hai ẩn: $ \left\{ \begin{array}{l}ax+by=c\\a’x+b’y=c’\end{array} \right.$ trong đó a, b, c, a’, b’, c’ ∈ R
• Minh họa tập nghiệm của hệ hai phương trình bậc nhất hai ẩn

Gọi (d): ax + by = c, (d’): a’x + b’y = c’, khi đó ta có

• (d) // (d’) thì hệ vô nghiệm
• (d) (d’) = thì hệ có nghiệm duy nhất
• (d) $ \equiv $ (d’) thì hệ có vô số nghiệm

• Hệ phương trình tương đương

Hệ hai phương trình tương đương với nhau nếu chúng có cùng tập nghiệm

c. Giải hệ phương trình bằng phương pháp thế

• Quy tắc thế
• Giải hệ phương trình bằng phương pháp thế
  • Dùng quy tắc thế biến đổi hệ phương trình đã cho để được một hệ phương trình mới trong đó có một phương trình một ẩn
  • Giải phương trình một ẩn vừa có rồi suy ra nghiệm của hệ

d. Giải hệ phương trình bằng phương pháp cộng đại số

– Quy tắc cộng

– Giải hệ phương trình bằng phương pháp thế

+ Nhân hai vế của mỗi phương trình với một số thích hợp (nếu cần) sao cho các hệ số của một ẩn nào đó trong hai phương trình bằng nhau hoặc đối nhau

+ Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (phương trình một ẩn)

+ Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho

A.2 Hệ phương trình đưa về phương trình bậc hai

– Nếu hai số x và y thỏa mãn x + y = S, x.y = P (với S² ≥ 4P) khi đó hai số x, y là nghiệm của phương trình: x² + SX + P = 0

A.3 Kiến thức bổ xung

A.3.1. Hệ phương trình đối xứng loại 1

a. Định nghĩa:
Hệ hai phương trình hai ẩn x và y được gọi là đối xứng loại 1 nếu ta đổi chỗ hai ẩn x và y đó thì từng phương trình của hệ không đổi

b. Cách giải

• Đặt S = x + y, P = x.y, Đk: S² 4P
• Giải hệ để tìm S và P
• Với mỗi cặp (S, P) thì x và y là hai nghiệm của phương trình:
  t² – St + P = 0

c. Ví dụ giải hệ phương trình:

$ \left\{ \begin{array}{l}x+y+xy=7\\{{x}^{2}}+{{y}^{2}}+xy=13\end{array} \right.$

$ \left\{ \begin{array}{l}x+y+xy+1=0\\{{x}^{2}}+{{y}^{2}}-x-y=22\end{array} \right.$

$ \left\{ \begin{array}{l}x+y+{{x}^{2}}+{{y}^{2}}=8\\xy(x+1)(y+1)=12\end{array} \right.$

A.3.2. Hệ phương trình đối xứng loại 2

a. Định nghĩa

Hệ hai phương trình hai ẩn x và y được gọi là đối xứng loại 2 nếu ta đổi chỗ hai ẩn x và y thì phương trình này trở thành phương trình kia và ngược lại

b. Cách giải

• Trừ vế theo vế hai phương trình trong hệ để được phương trình hai ẩn
• Biến đổi phương trình hai ẩn vừa tìm được thành phương trình tích
• Giải phương trình tích ở trên để biểu diễn x theo y (hoặc y theo x)
• Thế x bởi y (hoặc y bởi x) vào 1 trong 2 phương trình trong hệ để được phương trình một ẩn
• Giải phương trình một ẩn vừa tìm được ròi suy ra nghiệm của hệ

c. Ví dụ

Giải hệ phương trình:

$ \displaystyle \left\{ \begin{array}{l}2x={{y}^{2}}-4y+5\\2y={{x}^{2}}-4x+5\end{array} \right.$

$ \left\{ \begin{array}{l}{{x}^{3}}=13x-6y\\{{y}^{3}}=13y-6x\end{array} \right.$

A.3.3.Hệ phương trình đẳng cấp bậc 2

a. Định nghĩa

– Hệ phương trình đẳng cấp bậc hai có dạng:

b. Cách giải

• Xét xem x = 0 có là nghiệm của hệ phương trình không
• Nếu x 0, ta đặt y = tx rồi thay vào hai phương trình trong hệ
• Khử x rồi giải hệ tìm t
• Thay y = tx vào một trong hai phương trình của hệ để được phương trình một ẩn (ẩn x)
• Giải phương trình một ẩn trên để tìm x từ đó suy ra y dựa vào y = tx

* Lưu ý: ta có thể thay x bởi y và y bởi x trong phần trên để có cách giải tương tự

c. Ví dụ

Giải hệ phương trình:

$ \left\{ \begin{array}{l}{{x}^{2}}-4xy+{{y}^{2}}=1\\{{y}^{2}}-3xy=4\end{array} \right.$

$ \left\{ \begin{array}{l}2{{x}^{2}}-3xy+{{y}^{2}}=3\\{{x}^{2}}+2xy-2{{y}^{2}}=6\end{array} \right.$

CÁCH GIẢI HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Dạng 1: Giải hệ phương trình có bản và đưa về dạng cơ bản

1. Vận dụng quy tắc thế và quy tắc cộng đại số để giải các hệ phương trình sau:

– Giải hệ phương trình bằng phương pháp thế

– Giải hệ phương trình bằng phương pháp cộng đại số

2. Bài tập

Dạng 2: Giải các hệ phương trình sau bằng cách đặt ẩn số phụ

Bài tập:

Dạng 3: Giải và biện luận hệ phương trình

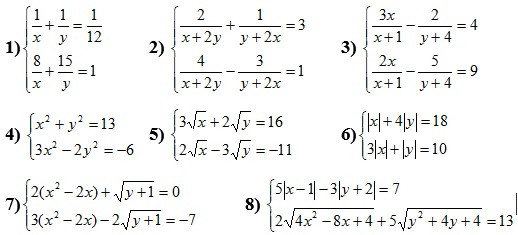
Phương pháp giải:

• Từ một phương trình của hệ tìm y theo x rồi thế vào phương trình thứ hai để được phương trình bậc nhất đối với x
• Giả sử phương trình bậc nhất đối với x có dạng: ax = b (1)
• Biện luận phương trình (1) ta sẽ có sự biện luận của hệ

i) Nếu a = 0: (1) trở thành 0x = b

          – Nếu b = 0 thì hệ có vô số nghiệm

          – Nếu b0 thì hệ vô nghiệm

ii) Nếu a 0 thì (1) x = , Thay vào biểu thức của x ta tìm y, lúc đó hệ phương trình có nghiệm duy nhất.

Bài tập: Giải và biện luận các hệ phương trình sau:

Dạng 4: Xác định giá trị của tham số để hệ có nghiệm thỏa mãn điều kiện cho trước

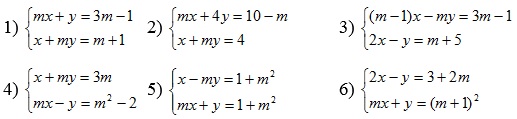
Phương pháp giải:

• Giải hệ phương trình theo tham số
• Viết x, y của hệ về dạng: $ \displaystyle n+\frac{k}{f(m)}$ với n, k nguyên
• Tìm m nguyên để f(m) là ước của k

Ví dụ 1: Xác định m nguyên để hệ có nghiệm duy nhất là nghiệm nguyên:

$ \displaystyle \left\{ \begin{array}{l}mx+2y=m+1\\2x+my=2m-1\end{array} \right.$

Giải

Bài tập:

Bài 1: Định m nguyên để hệ có nghiệm duy nhất là nghiệm nguyên:

$ \displaystyle \left\{ \begin{array}{l}(m+1)x+2y=m-1\\m_{{}}^{2}x-y=m_{{}}^{2}+2m\end{array} \right.$

Bài 2:

a) Định m, n để hệ phương trình sau có nghiệm là (2; -1)

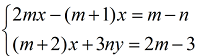
HD: Thay x = 2 ; y = -1 vào hệ ta được hệ phương trình với ẩn m, n

b) Định a, b biết phương trình ax² -2bx + 3 = 0 có hai nghiệm là x = 1 và x = -2

HD: Thay x = 1 và x = -2 vào phương trình ta được hệ phương trình với ẩn a, b

c) Xác định a, b để đa thức f(x) = 2ax² + bx – 3 chia hết cho 4x – 1 và x + 3

Bài 3: Xác định a, b để đường thẳng y = ax + b đi qua hai điểm A(2 ; 1) ; B(1 ; 2)

HD: Đường thẳng  y = ax + b đi qua hai điểm A(2 ; 1) ; B(1 ; 2) ta có hệ phương trình

Bài 4: Định m để 3 đường thẳng  3x + 2y = 4; 2x – y = m và x + 2y = 3 đồng quy

HD:

– Tọa độ giao điểm M (x ; y) của hai đường thẳng 3x + 2y = 4 và x + 2y = 3 là nghiệm của hệ phương trình: $ \displaystyle \left\{ \begin{array}{l}3x+2y=4\\x+2y=3\end{array} \right.\Leftrightarrow \left\{ \begin{array}{l}x=0,5\\y=1,25\end{array} \right.$ .

Vậy M(0,2 ; 1,25)

Để ba đường thẳng trên đồng quy thì điểm M thuộc đường thẳng 2x – y = m, tức là: 2.0,2- 1,25 = m ⇔ m = -0,85

Vậy khi m = -0,85 thì ba đường thẳng trên đồng quy

Định m để 3 đường thẳng sau đồng quy

a) 2x – y = m ; x – y = 2m ;  mx – (m – 1)y = 2m – 1

b) mx + y = m² + 1 ; (m +2)x – (3m + 5)y = m – 5 ; (2 – m)x – 2y = -m² + 2m – 2

Bài 5: Định m để hệ phương trình có nghiệm duy nhất (x;y) thỏa mãn hệ thức cho trước

Cho hệ phương trình: $ \displaystyle \left\{ \begin{array}{l}mx+4y=9\\x+my=8\end{array} \right.$

Với giá trị nào của m để hệ có nghiệm (x ; y) thỏa mãn hệ thức:

$ \displaystyle 2x+y+\frac{38}{m_{{}}^{2}-4}=3$

HD: 

Giải hệ phương trình theo m ( m ≠ ± 2) sau đó thế vào hệ thức.

BÀI TẬP CHUYÊN ĐỀ HỆ PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN

Bài 1: Cho hệ phương trình $ \displaystyle \left\{ \begin{array}{l}mx+4y=10-m\\x+my=4\end{array} \right.$ (m là tham số)

a) Giải hệ phương trình khi m = $ \displaystyle \sqrt{2}$

b) Giải và biện luận hệ phương trình theo m

c) Xác định các giá trị nguyên của m để hệ có nghiệm duy nhất (x;y) sao cho x> 0, y > 0

d) Với giá trị nào của m thì hệ có nghiệm (x;y) với x, y là các số nguyên dương

Bài 2: Cho hệ phương trình: $ \displaystyle \left\{ \begin{array}{l}(m-1)x-my=3m-1\\2x-y=m+5\end{array} \right.$

a) Giải và biện luận hệ phương trình theo m

b) Với giá trị nguyên nào của m để hai đường thẳng của hệ cắt nhau tại một điểm nằm trong góc phần tư thứ IV của hệ tọa độ Oxy

c) Định m để hệ có nghiệm duy nhất (x ; y) sao cho P = x² + y² đạt giá trị nhỏ nhất.

Bài 3: Cho hệ phương trình: $ \displaystyle \left\{ \begin{array}{l}3x+2y=4\\2x-y=m\end{array} \right.$

a) Giải hệ phương trình khi m = 5

b) Tìm m nguyên sao cho hệ có nghiệm (x; y) với x < 1, y < 1

c) Với giá trị nào của m thì ba đường thẳng

3x + 2y = 4; 2x – y = m; x + 2y = 3 đồng quy

Bài 4: Cho hệ phương trình: $ \displaystyle \left\{ \begin{array}{l}mx+4y=9\\x+my=8\end{array} \right.$

a) Giải hệ phương trình khi m = 1

b) Với giá trị nào của m để hệ có nghiệm (-1 ; 3)

c) Với giá trị nào của m thì hệ có nghiệm duy nhất, vô nghiệm

 Bài 5: Cho hệ phương trình: $ \displaystyle \left\{ \begin{array}{l}x+my=9\\mx-3y=4\end{array} \right.$

a) Giải hệ phương trình khi m = 3

b) Với giá trị nào của m để hệ có nghiệm (-1 ; 3)

c) Chứng tỏ rằng hệ phương trình luôn luôn có nghiệm duy nhất với mọi m

d) Với giá trị nào của m để hệ có nghiệm (x ; y) thỏa mãn hệ thức:

$ \displaystyle x-3y=\frac{28}{m_{{}}^{2}+3}-3$

Bài 6: Cho hệ phương trình: $ \displaystyle \left\{ \begin{array}{l}mx-y=2\\3x+my=5\end{array} \right.$

a) Giải hệ phương trình khi $ \displaystyle m=\sqrt{2}$ .

b) Tìm giá trị của m để hệ phương trình đã cho có nghiệm (x; y) thỏa mãn hệ thức $ \displaystyle x+y=1-\frac{m_{{}}^{2}}{m_{{}}^{2}+3}$ .

Bài 7: Cho hệ phương trình: $ \displaystyle \left\{ \begin{array}{l}3x-my=2=-9\\mx+2y=16\end{array} \right.$

a) Giải hệ phương trình khi m = 5

b) Chứng tỏ rằng hệ phương trình luôn luôn có nghiệm duy nhất với mọi m

c) Định m để hệ có nghiệm (x ; y) = ( 1,4 ; 6,6)

d) Tìm giá trị nguyên của m để hai đường thẳng của hệ cắt nhau tại một điểm nằm trong góc phần tư thứ IV trên mặt phẳng tọa độ Oxy

e) Với trị nguyên nào của m để hệ có nghiệm (x ; y) thỏa mãn x + y = 7