Thời gian làm bài 120 phút, không kể thời gian giao đề.
Đề thi:
Câu 1 (1,5 điểm)
a) Giải phương trình: $ \frac{x+1}{2}-1=0$.
b) Giải hệ phương trình: $ \left\{ \begin{array}{l}2x-y=3\\{{x}^{2}}+y=5\end{array} \right.$.
Câu 2 (2,5 điểm)
Trong mặt phẳng tọa độ Oxy cho parabol (P) có phương trình $ y=\frac{1}{2}{{x}^{2}}$ và hai điểm A, B thuộc (P) có hoành độ lần lượt là $ {{x}_{A}}=-1;{{x}_{B}}=2$.
a) Tìm tọa độ của hai điểm A, B.
b) Viết phương trình đường thẳng (d) đi qua hai điểm A, B.
c) Tính khoảng cách từ O (gốc tọa độ) đến đường thẳng (d).
Câu 3 (2,0 điểm)
Cho phương trình: $ {{x}^{2}}-2(m+1)x+{{m}^{2}}+m-1=0$ (m là tham số).
a) Giải phương trình với $ \displaystyle m=0$.
b) Tìm m để phương trình có hai nghiệm phân biệt $ \displaystyle {{x}_{1}},\ {{x}_{2}}$ thỏa mãn điều kiện:
$ \frac{1}{{{x}_{1}}}+\frac{1}{{{x}_{2}}}=4$.
Câu 4 (3,0 điểm)
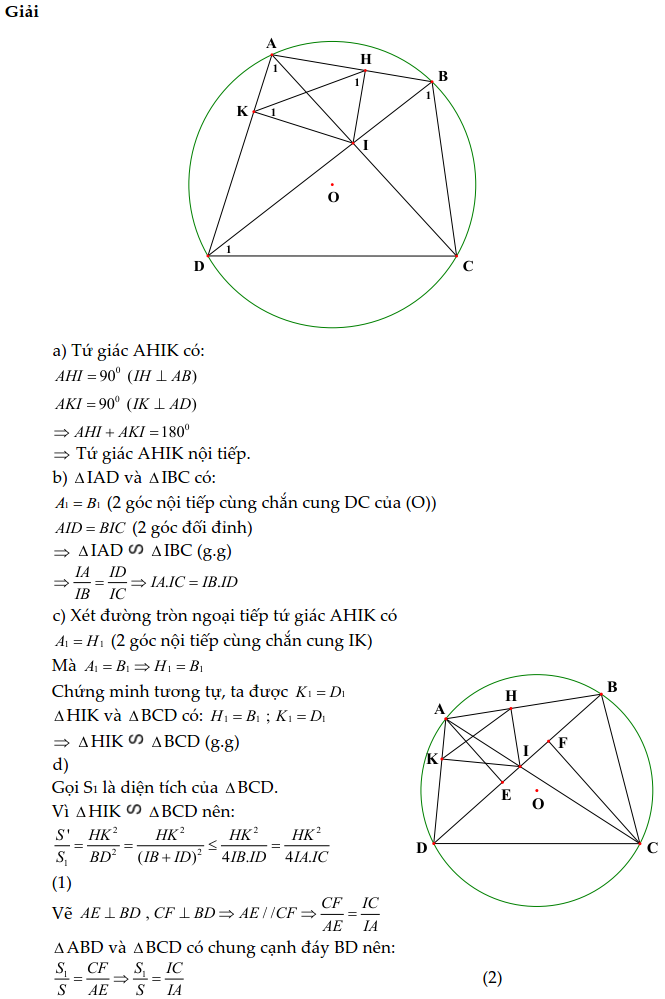
Cho tứ giác ABCD nội tiếp đường tròn (O; R). Gọi I là giao điểm AC và BD. Kẻ IH vuông góc với AB; IK vuông góc với AD ($ H\in AB;K\in AD$).
a) Chứng minh tứ giác AHIK nội tiếp đường tròn.
b) Chứng minh rằng IA.IC = IB.ID.
c) Chứng minh rằng tam giác HIK và tam giác BCD đồng dạng.
d) Gọi S là diện tích tam giác ABD, S’ là diện tích tam giác HIK. Chứng minh rằng:
$ \frac{S’}{S}\le \frac{H{{K}^{2}}}{4.A{{I}^{2}}}$
Câu 5 (1,0 điểm)
Giải phương trình : $ {{\left( {{x}^{3}}-4 \right)}^{3}}={{\left( \sqrt[3]{{{({{x}^{2}}+4)}^{2}}}+4 \right)}^{2}}$.