Bài I (2,0 điểm)
Cho hai biểu thức A = $ \displaystyle \frac{{\sqrt{x}+4}}{{\sqrt{x}-1}}$ và B = $ \displaystyle \frac{{3\sqrt{x}+1}}{{x+2\sqrt{x}-3}}-\frac{2}{{\sqrt{x}+3}}$ với x ≥ 0, x ≠ 1
1) Tính giá trị của biểu thức A khi x = 9.
2) Chứng minh B = $ \displaystyle \frac{1}{{\sqrt{x}-1}}$
3) Tìm tất cả giá trị của x để $ \displaystyle \frac{A}{B}\ge \frac{x}{4}+5$.
Bài II (2,0 điểm)
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một mảnh đất hình chữ nhật có chu vi bằng 28 mét và độ dài đường chéo bằng 10 mét. Tính chiều dài và chiều rộng của mảnh đất đó theo đơn vị mét.
Bài III (2,0 điểm)
1) Giải hệ phương trình $ \displaystyle \left\{ \begin{array}{l}4x-\left| {y+2} \right|=3\\x+2\left| {y+2} \right|=3\end{array} \right.$.
2) Trong mặt phẳng tọa độ Oxy, cho đường thẳng (d): y = (m + 2)x + 3 và parabol (P): y = x2.
a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt.
b) Tìm tất cả các giá trị của m để (d) cắt (P) tại hai điểm phân biệt có các hoành độ là các số nguyên.
Bài IV (3,5 điểm)
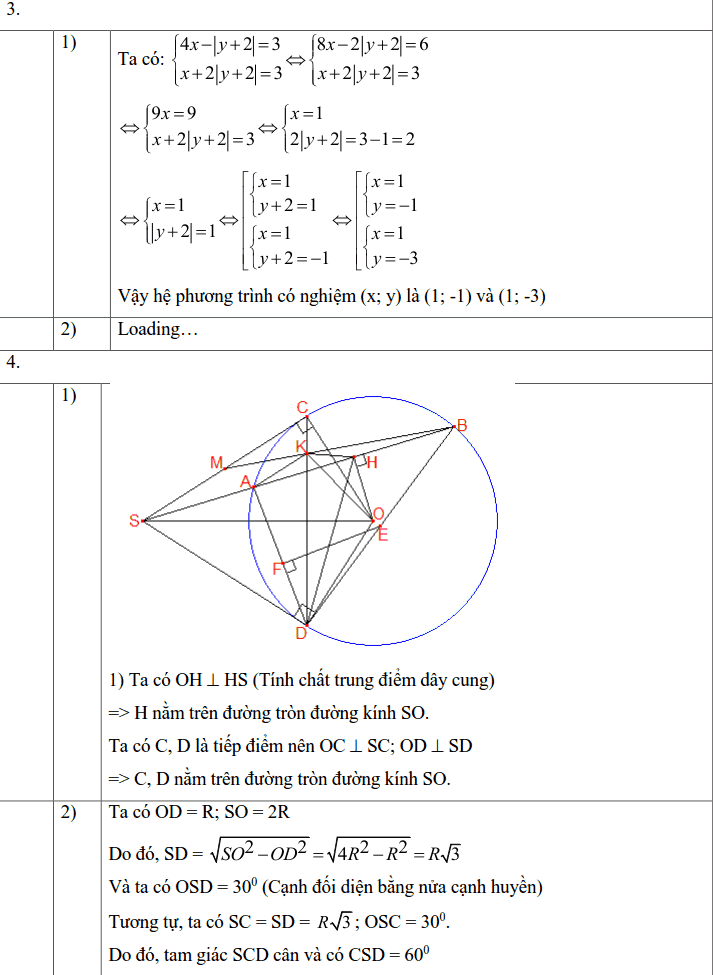
Cho đường tròn (O; R) với dây cung AB không đi qua tâm. Lấy S là một điểm bất kì trên tia đối của tia AB (S khác A). Từ điểm S vẽ hai tiếp tuyến SC, SD với đường tròn (O; R) sao cho điểm C nằm trên cung nhỏ AB (C, D là các tiếp điểm). Gọi H là trung điểm của đoạn thẳng AB.
1) Chứng minh năm điểm C, D, H, O, S thuộc đường tròn đường kính SO.
2) Khi SO = 2R, hãy tính độ dài đoạn thẳng SD theo R và tính số đo $ \displaystyle \widehat{{CSD}}$.
3) Đường thẳng đi qua điểm A và song song với đường thẳng SC, cắt đoạn thẳng CD tại điểm K. Chứng minh tứ giác ADHK là tứ giác nội tiếp và đường thẳng BK đi qua trung điểm của đoạn thẳng SC.
4) Gọi E là trung điểm của đoạn thẳng BD và F là hình chiếu vuông góc của điểm E trên đường thẳng AD. Chứng minh rằng, khi điểm S thay đổi trên tia đối của tia AB thì điểm F luôn thuộc một đường tròn cố định.
Bài V (0,5 điểm)
Tìm giá trị nhỏ nhất của biểu thức P = $ \displaystyle \sqrt{{1-x}}+\sqrt{{1+x}}+2\sqrt{x}$.