Bài tập tuần 1 – Toán lớp 9

BÀI TẬP TUẦN 1
– Căn thức bậc hai $\displaystyle \sqrt{{{A}^{2}}}=\left| A \right|$
– 1 số hệ thức cạnh và đường cao trong tam giác vuông
Bài 1: So sánh

a) 5 và $\displaystyle \sqrt{26}$

b) $\displaystyle -\sqrt{26}$ và $\displaystyle -\sqrt{29}$

c) $\displaystyle \sqrt{37}+\sqrt{10}$ và $\displaystyle \sqrt{80}$

Bài 2: Tính giá trị biểu thức:

a) $\displaystyle \sqrt{\frac{25}{49}}-\sqrt{\frac{1}{16}}+\sqrt{{{(-2)}^{2}}}$

b) $\displaystyle {{\left( \sqrt{3} \right)}^{2}}\sqrt{0,25}-0,2\sqrt{{{\left( -3 \right)}^{2}}}$

c) $\displaystyle \sqrt{{{113}^{2}}-{{112}^{2}}}$

d) $\displaystyle \sqrt{{{\left( -0,1 \right)}^{4}}}+\sqrt{{{58}^{2}}-{{42}^{2}}}$

e) $\displaystyle \sqrt{{{\left( \sqrt{10}-3 \right)}^{2}}}+\sqrt{{{\left( \sqrt{10}-4 \right)}^{2}}}$

f) $\displaystyle \sqrt{11+6\sqrt{2}}+\sqrt{11-6\sqrt{2}}$

g)$\displaystyle \sqrt{29+12\sqrt{5}}+\sqrt{29-12\sqrt{5}}$

Bài 3: Tìm x để biểu thức sau có nghĩa

a) $\displaystyle \sqrt{3x-1}$

b) $\displaystyle \sqrt{\frac{2}{x-1}}$

c) $\displaystyle \sqrt{5+{{x}^{2}}}$

d)$\displaystyle \sqrt{\frac{x-1}{2x-4}}$

Bài 4: Tìm x, biết:

a) $\displaystyle \sqrt{{{x}^{2}}}=\left| -7 \right|$

b) $\displaystyle \frac{\sqrt{9-4\sqrt{5}}}{2-\sqrt{5}}$$\displaystyle \sqrt{36{{x}^{2}}}=10$

c) $\displaystyle \sqrt{4{{x}^{2}}-4x+1}=5$

d) $\displaystyle \sqrt{{{x}^{2}}-4x+25}=5$

e) $\displaystyle \sqrt{x}<2$

f) $\displaystyle \frac{4-2\sqrt{x}}{\sqrt{x}+1}>0$

g*) $\displaystyle \sqrt{x+4\sqrt{x-4}}=2$

h*) $\displaystyle \sqrt{2x-2+2\sqrt{2x-3}}+\sqrt{2x+13+8\sqrt{2x-3}}=5$

Bài 5: Phân tích đa thức thành nhân tử, rút gọn biểu thức:

a) x² – 10

b) $\displaystyle x-4\sqrt{x}+4$

c) $\displaystyle \frac{x-6\sqrt{x}+9}{x-9}$

d) $\displaystyle \frac{\sqrt{9-4\sqrt{5}}}{2-\sqrt{5}}$

e*) $\displaystyle \frac{\sqrt{9+2\sqrt{2}+2\sqrt{3}+2\sqrt{2}\sqrt{3}}}{6+3\sqrt{2}+3\sqrt{3}}$

Bài 6*: Tìm x,y,z biết: $\displaystyle \frac{x+y+z}{2}-3020=\sqrt{x-2017}+2\sqrt{y-2018}+3\sqrt{z-2019}$

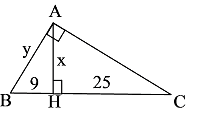
Bài 7: Tìm x, y có trên hình vẽ sau :

Bài 8: Cho tam giác ABC, đường cao AH, biết AB2 = BH.BC. Chứng minh tam giác ABC vuông.

Bài 9: Cho ΔABC vuông tại A, đường cao AH. Biết HB = 3,6cm ; HC = 6,4cm

a)Tính độ dài các đoạn thẳng: AB, AC, AH.

b) Kẻ HE$\displaystyle \bot$AB ; HF$\displaystyle \bot$AC. Chứng minh rằng: AB.AE = AC.AF

Bài 10: Cho tam giác ABC vuông ở A, phân giác AD, đường cao AH. Biết CD = 68cm, BD = 51cm. Tính BH, HC.

Bài 11: Cho hình thang ABCD có $\displaystyle \widehat{B}\text{ = }\widehat{\text{C}}\text{ = 9}{{\text{0}}^{\text{o}}}$, hai đường chéo vuông góc với nhau tại H. Biết rằng AB = $\displaystyle 3\sqrt{5}$cm; HA = 3cm. Chứng minh rằng:

a) HA : HB : HC : HD = 1 : 2 : 4 : 8

b) $\displaystyle \frac{\text{1}}{\text{A}{{\text{B}}^{\text{2}}}}-\frac{\text{1}}{\text{C}{{\text{D}}^{\text{2}}}}=\frac{\text{1}}{\text{H}{{\text{B}}^{\text{2}}}}-\frac{\text{1}}{\text{H}{{\text{C}}^{\text{2}}}}$