
Bài 1: Cho hình vẽ:
a) Viết tọa độ các điểm A, B, C, D;
b) Có nhận xét gì về tọa độ các điểm A và B; C và D.
Bài 2: Hàm số $ y=f\left( x \right)$ được cho bởi công thức $ y=\frac{{16}}{{x-2}}$.
Tìm các giá trị của x sao cho vế phải công thức có nghĩa.
Hãy điền các giá trị tương ứng của hàm số $ y=f\left( x \right)$ vào bảng sau:
| x | -6 | -3 | -2 | -1 | 1 | 3 | 6 | 10 |
| y |
Bài 3: Hàm số y = f(x) được xác định bởi tập hợp:
$ \left\{ {\left( {-3;12} \right);\left( {-2;8} \right);\left( {-1;4} \right);\left( {0;0} \right);\left( {1;-4} \right);\left( {2;-8} \right);\left( {3;-12} \right)} \right\}$
a) Lập bảng giá trị tương ứng x và y của hàm số trên.
b) Hàm số trên có thể được viết bởi công thức nào?
Bài 4: Cho hàm số $ y=f\left( x \right)=\frac{3}{2}x.$
Tính $ f\left( 0 \right);f\left( {-1} \right);f\left( 3 \right);f\left( {-3} \right);f\left( {\frac{1}{2}} \right);f\left( {-\frac{1}{2}} \right);f\left( {\frac{3}{2}} \right);f\left( {-\frac{3}{2}} \right).$
Bài 5: Cho hàm số $ y=f\left( x \right)=2x.$
a) Viết năm cặp số $ \left( {x;y} \right)$ với $ x=-2;-1;0;1;2;$
b) Biểu diễn các cặp điểm trên cùng mặt phẳng tọa độ;
c) Vẽ đường thẳng đi qua hai điểm ( – 2 ; – 4) và ( 2 ; 4 ). Kiểm tra bằng thước thẳng xem các điểm còn lại có nằm trên đường thẳng đó không?
Bài 6: Cho góc xOy nhọn, tia Ot là phân giác của góc xOy. Trên tia Ot lấy điểm I. Vẽ $ IH\bot Ox,~IK\bot Oy~~(~H\in Ox,~$K$ \in Oy~).$ Chứng minh OH =OK.
Bài 7: Cho hình vẽ:
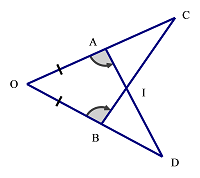
Giả sử OA = OB, $ \widehat{{OAD}}=\widehat{{OBC}}.$
a) Chứng minh AD =BC.
b) Chứng minh $ \Delta IAC=\Delta IBD.$
Bài 8: Cho tam giác ABC có $ \hat{B}=\hat{C}.~$Tia phân giác của góc B cắt AC tại D, tia phân giác của góc C cắt AB tại E. Chứng minh BD = CE.
Bài 9: Cho tia Oz là phân giác của góc xOy. Trên Oz lấy điểm D, kẻ $ DH\bot Ox~\left( {~H\in Ox~} \right),$ kẻ $ DK\bot Oy~\left( {~K\in Oy~} \right).$
a) Chứng minh $ \Delta ODH=\Delta ODK.$
b) HD cắt tia Oy tại A, KD cắt tia Ox tại B. Chứng minh $ \displaystyle \Delta HDB=\Delta KDA.$
c) Chứng minh OA = OB.
Bài 10: Cho I là trung điểm của đoạn thẳng AB. Trên hai nửa mặt phẳng bờ AB vẽ hai tia Ax // By. Trên tia By lấy điểm M, MI cắt Ax tại N.
a) Chứng minh AN = BM.
b) Nối BN, AM. Chứng minh BN = AM, BN // AM.