

Bài 1: Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau:
a) $~\left( {{{d}_{1}}} \right):y=x;$
b) $~\left( {{{d}_{2}}} \right):y=-x;$
c) $~\left( {{{d}_{3}}} \right):y=-2x;$
d) $~\left( {{{d}_{4}}} \right):y=-3x.$
Bài 2: Đồ thị hàm số y = ax ( a$ \ne $0 ) là đường thẳng OA trong hình bên.
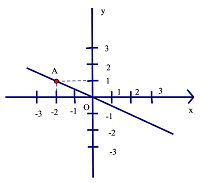
a) Hãy xác định hệ số a;
b) Đánh dấu điểm trên đồ thị có hoành độ là 2;
c) Đánh dấu điểm trên đồ thị có tung độ là 2.
Bài 3: Cho hàm số $ y=\frac{1}{3}x$ và các điểm A, B, C, D thuộc đồ thị hàm số.
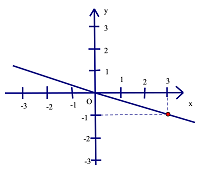
a) Tìm tọa độ của điểm A và B biết hoành độ điểm A là 1, hoành độ điểm B là $ -\frac{3}{2}.$
b) Tìm tọa độ điểm C và D biết tung độ điểm C là 0, tung độ điểm D là $ \frac{9}{4}.$
Bài 4: Cho hình vẽ bên.
a) Viết hàm số có đồ thị là đường thẳng OM;
b) Trong các điểm sau điểm nào thuộc đường thẳng OM? Giải thích.
c) $ A\left( {0;3} \right);B\left( {-1;3} \right);C\left( {3;-1} \right);D\left( {-\frac{1}{2};-1} \right);E\left( {\frac{3}{2};-\frac{3}{4}} \right);F\left( {-\frac{3}{4};\frac{1}{4}} \right).$
Bài 5:
a) Biết điểm A(a;9) thuộc đồ thị hàm số y = -4,5x. Tìm giá trị của a;
b) Biết điểm B (0,25;-b) thuộc đồ thị hàm số $ y=\frac{1}{5}x$. Tìm giá trị của b.
Bài 6: Cho góc nhọn xOy như hình vẽ:
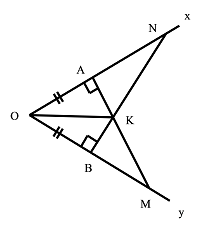
Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Từ A kẻ đường thẳng vuông góc với Ox cắt Oy tại M, từ B kẻ đường thẳng vuông góc với Oy cắt Ox tại N. AM cắt BN tại K. Chứng minh:
a) $ \Delta AKN=\Delta BKM$;
b) OK là phân giác của góc AOB.
Bài 7: Cho $ \Delta ABC$ vuông tại A, M là trung điểm của BC. Trên tia AM lấy điểm D sao cho M là trung điểm của AD. Chứng minh:
a) $~CD=AB,$ CD // AB; b) $~AM=\frac{1}{2}BC.$
Bài 8: Cho góc xAy bằng $ {{60}^{o}}$, tia phân giác Az. Lấy điểm B trên tia Az. Qua B vẽ đường thẳng song song với Ay cắt Ax tại C, đường thẳng song song với Ax cắt Ay tại D.
a) Chứng minh AC = AD, BC = BD.
b) Kẻ $ BH\bot Ax,~BK\bot Ay$. Chứng minh BH = BK.
c) Tính số đo góc HBK.
Bài 9: Cho góc xOy, H thuộc phân giác Oz. Một đường thẳng qua H vuông góc với Oz cắt Ox và Oy tại A và B.
a) Chứng minh OA = OB;
b) Từ A kẻ AC // Oy ( C thuộc tia Oz ). Chứng minh AC = OA.
Bài 10: Cho $ \Delta ABC$ có góc A nhọn, AB = AC. Kẻ $ CD\bot AB~\left( {~D\in AB} \right),$ kẻ $ BE\bot AC~\left( {E\in AC} \right)$. Gọi O là giao điểm của BE và CD. Chứng minh :
a) BE = CD;
b) OD = OE và OB = OC;
c) AO là phân giác của góc BAC.