
BÀI TẬP TUẦN 7: Rút gọn biểu thức chứa căn bậc hai
Bài 1: Đưa các số (biểu thức) ra ngoài dấu căn:
a) $ \sqrt{8{{m}^{2}}{{n}^{3}}}$ với $ m\ge 0\,;\,\,n\ge 0$
b) $ \sqrt{50{{p}^{2}}{{q}^{3}}}$ với $ q\ge 0$
c) $ \sqrt{8{{m}^{3}}{{n}^{2}}}$ với $ m\ge 0\,;\,\,n\ge 0$
d) $ \sqrt{27{{a}^{3}}{{b}^{5}}}$ với $ a\ge 0\,;\,\,b\ge 0$
Bài 2: Đưa thừa số vào trong dấu căn:
a) $ -10\sqrt{2}$
b) $ \frac{3}{4}\sqrt{\frac{8}{3}}$
c) $ -5\sqrt{3}$
d) $ k\sqrt{\frac{2}{k}}$ với k > 0
Bài 3: So sánh
a) $ \sqrt{196-36}\,\,v\grave{a}\,\,\sqrt{196}-\sqrt{36}$
b) $ \sqrt{14-6\sqrt{5}}\,\,v\grave{a}\,\,\sqrt{5}-3$
c) $ \sqrt{3+\sqrt{5}}+\sqrt{3-\sqrt{5}}\,\,v\grave{a}\,\,2+\sqrt{5}$
Bài 4: Rút gọn
a) $ A=\left( n\sqrt{\frac{6}{n}}+\sqrt{\frac{2n}{3}}+\sqrt{6n} \right):\sqrt{6}n$ với n > 0
b) $ B=\frac{1}{m-3\sqrt{m}+2}+\frac{1}{\sqrt{m}-1}-\frac{1}{2-\sqrt{m}}$ với $ m\ge 0;\,\,m\ne 1;\,\,m\ne 2$
c) $ C=\frac{1}{3m-1}\sqrt{3{{m}^{2}}\left( 9{{m}^{2}}-6m+1 \right)}$ với $ 0<m<\frac{1}{3}$
d) $ D=\left[ \frac{{{\left( \sqrt{a}+\sqrt{b} \right)}^{2}}-4\sqrt{ab}}{\sqrt{a}-\sqrt{b}} \right]:\frac{\sqrt{ab}}{\sqrt{{{a}^{2}}b}+\sqrt{a{{b}^{2}}}}$ với a > 0; b > 0 và $ a\ne b$
Bài 5: Giải phương trình sau:
a) $ 4\sqrt{2y}+10\sqrt{8y}-9\sqrt{18y}+20=-10$
b) $ \frac{3\sqrt{y}-6}{2}+\frac{2\sqrt{y}-5}{3}+1=\sqrt{y}$
c) $ \frac{1}{3}\sqrt{y-1}+\sqrt{16y-16}-12\sqrt{\frac{y-1}{25}}=\frac{29}{15}$
d) $ \frac{1}{y+\sqrt{1+{{y}^{2}}}}+\frac{1}{y-\sqrt{1+{{y}^{2}}}}+2=0$
Bài 6: Cho $ \Delta ABC$ vuông tại C như hình vẽ.
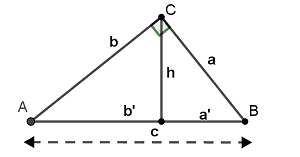
Biết $ \frac{a}{b}=2$ và h = 2. Hãy tìm a, b, c
Bài 7: Cho hình thang cân ABCD (AB // CD), có AB = 2cm và CD = 6cm. $ \widehat{D}=\alpha $ . Tính diện tích hình thang cân đó.
Bài 8: Cho $ \Delta ABC$ trong đó BC = 7cm, $ \widehat{ABC}={{42}^{0}}$ và $ \widehat{ACB}={{35}^{0}}$. Gọi H là chân đường cao của $ \Delta ABC$ kẻ từ A. Hãy tính AH (Làm trong kết quả đến chữ số thập phân thứ hai)
Bài 9: Cho $ \Delta ABC$ có BC = 12cm, $ \displaystyle \widehat{BAC}={{110}^{0}}$và $ \displaystyle \widehat{ABC}={{40}^{0}}$, đường cao AH, BH.
a) Tính BH, AB
b) Tính AC, AH
(Làm tròn kết quả đến chữ số thập phân thứ ba)