Bất đẳng thức Cosi – Toán Đại 9

Bất đẳng thức Cosi – Công thức, bài tập cơ bản và nâng cao

Bất đẳng thức Cosi xuất hiện rất nhiều trong các kỳ thi chuyển cấp. Vì thế chúng cần hiểu và vận dụng chúng để giải bài tập được tốt hơn. Bất đẳng thức này gồm 2 dạng trung bình cộng và trung bình nhân (AM – GM) Cauchy đã chứng minh

50 bài tập ứng dụng có lời giải. Tải PDF đầy đủ   TẠI ĐÂY   

Cuối bài mình có sưu tầm có nhiều tài liệu tổng hợp BĐT COSI rất hay. Mọi người tải đầy đủ nhé

Bài tập có hướng dẫn giải và phân tích những lỗi sai lầm thường gặp

1.1 Bất đẳng thức AM – GM

Cho x₁, x₂,…, x_n là n số lớn hơn không

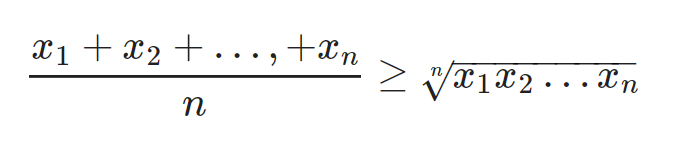
Điều này xảy ra khi: x₁ = x₂ =… = x_n

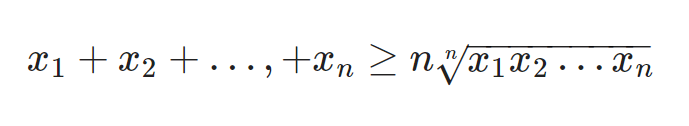Hoặc

Bất đẳng thức Cosi

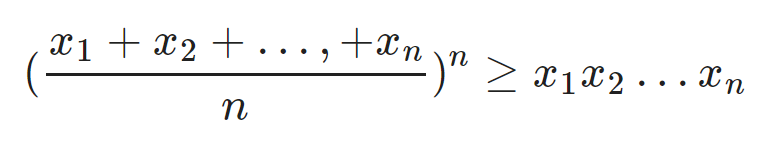
Với a₁ ,a₂,…, a_n  là các số thực bất kì và b₁, b₂,…, b_n là các số thực dương. Áp dụng những điều này ta có công thức

BĐT Cosi cho 2 số không âm

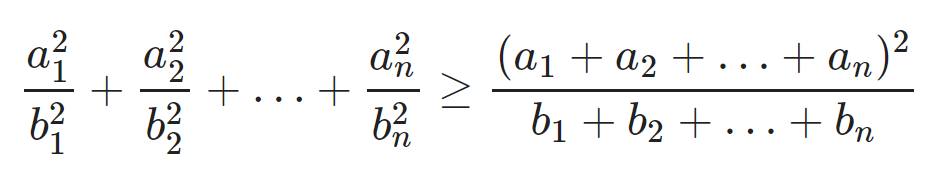
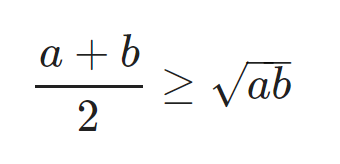
Dấu bằng xảy ra khi a = b

BĐT Cosi cho 3 số lớn hơn 0

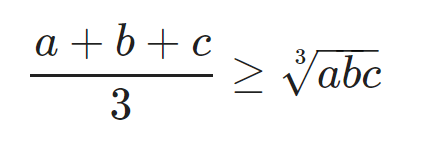
Dấu bằng xảy ra khi và chỉ khi a = b = c

BĐT Cosi cho n số không âm

Khi x₁, x₂,…, x_n là n những số thực không-âm, khi đó ta có:

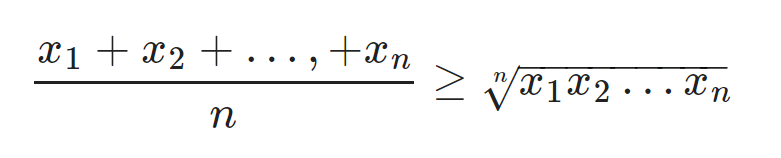
BĐT xảy ra  khi x₁ = x₂ =… = x_n

2. Chứng minh BĐT Cosi

Chứng minh bất BĐT Cosi  đúng với 2 thực số không âm

Rõ ràng với a = 0 và b = 0 thì bất đẳng thức luôn đúng (1). Ta chỉ cần chứng minh bất đẳng thức luôn đúng với 2 số a, b dương.

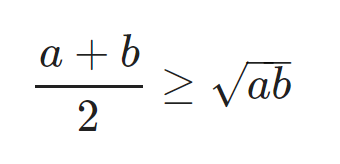
=> Bất đẳng thức đã cho luôn đúng với mọi a, b dương (2)

Từ (1) và (2) => bất đẳng thức cosi đúng với 2 số thực a, b không âm.

Chứng minh bất đẳng thức Cosi với 3 thực số không âm

Rõ ràng a = 0, b = 0, c = 0 thì bất đẳng thức luôn đúng. Do đó, ta chỉ cần chứng minh bất đẳng thức đúng với 3 số thực a, b, c dương.

=> x, y, z ≥ 0 => => x + y + z ≥ 0

Bất đẳng thức của 3 số thực a, b, c dương được quy về thành bất đẳng thức của 3 số thực x, y, z dương.

luôn đúng với mọi x, y, z ≥ 0

Dấu “=” xảy ra khi x = y = z hay a = b = c

2.3. Chứng minh bất đẳng thức Cosi với 4 số thực không âm

Ta dễ dàng nhận ra rằng với a = 0, b = 0, c = 0, d = 0 thì bất đẳng thức luôn đúng. Bây giờ chúng ta chỉ cần chứng minh bất đẳng thức đúng với 4 số thực dương. Từ kết quả chứng minh bất đẳng thức đúng với 2 số thực không âm ta có:

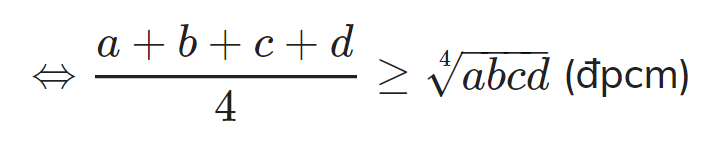
Ta còn rút ra được hệ quả:

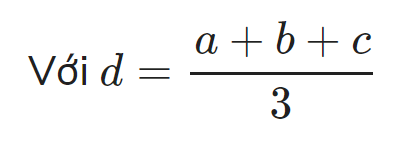
Thì bất đẳng thức trở về dạng bất đẳng thức cosi với 3 số thực dương.

Chứng minh bất đẳng thức Cosi với n số thực không âm

Nếu bất đẳng thức đúng với n số thì nó cũng đúng với 2n số. CM điều này như sau:

Theo quy nạp thì BĐT đúng với n là một lũy thừa của 2.

Mặt khác giả sử bất đẳng thức đúng với n số thì ta cũng chứng minh được nó đúng với n-1 số như sau:

Theo BĐT – Cosi cho n số:

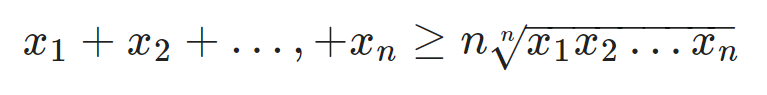
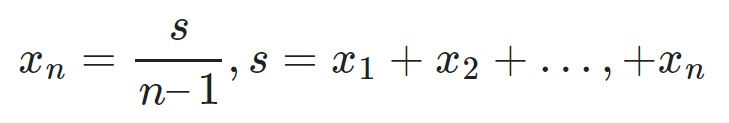
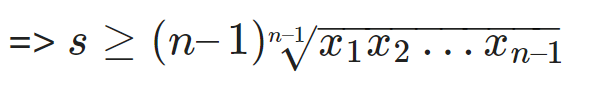
Đây chính là BĐT Cosi (n-1) số. Như vậy ta có dpcm.

Bài tập cơ bản về BĐT-cosi

Bài 1. Cho các số thực dương a, b, c thỏa mãn a² + b² + c² = 3.

Chứng minh rằng:

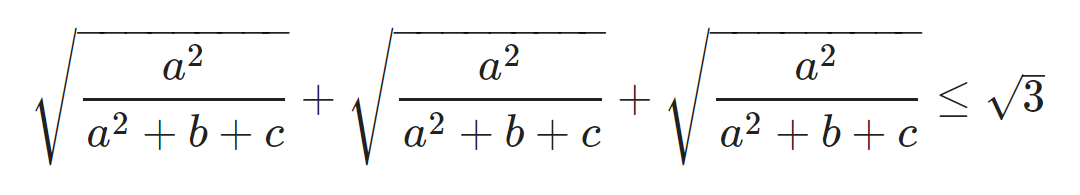
Giải:

Áp dụng BĐT Cosi, ta có:

Do đó, để chứng minh BĐT đã cho, ta chỉ cần chứng minh rằng:

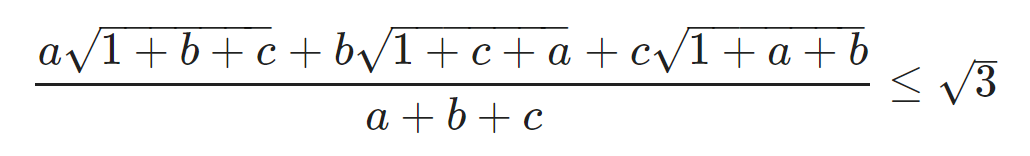
Giải BĐT Cosi lần 2 ta ca có

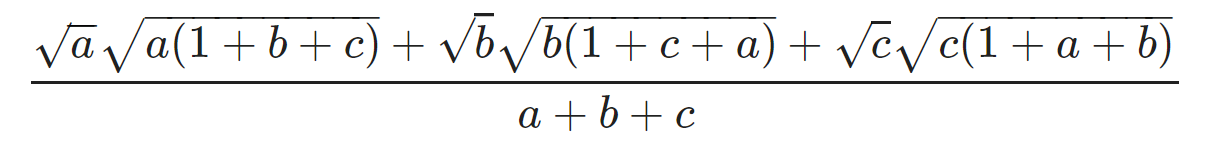
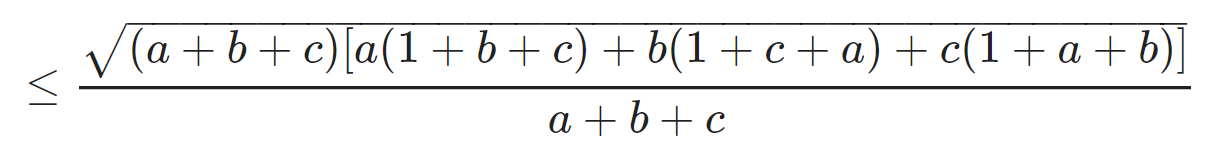
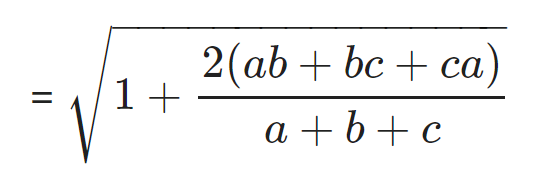
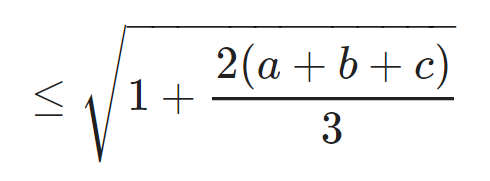
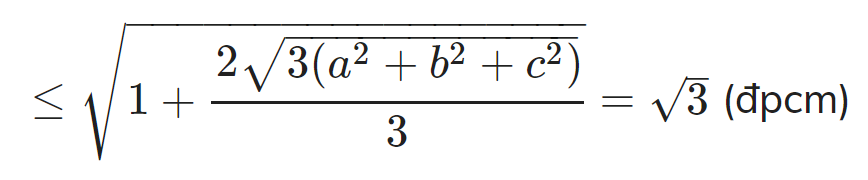
BĐT xảy ra khi và chỉ khi a = b = c = 1.

Bài tập nâng cao về bất đẳng thức cosi

Sách lý thuyết + bài tập ứng dụng cơ bản và nâng cao có lời giải về Bất Đẳng Thức Cosi

Tải PDF bằng MÁY TÍNH đầy đủ    TẠI ĐÂY