Các dạng toán về phép cộng và phép nhân – Toán lớp 6
A. TÓM TẮT LÍ THUYẾT.
1. Tổng và tích hai số tự nhiên
Phép cộng (kí hiệu “ ”) hai số tự nhiên bất kì cho ta một số tự nhiên duy nhất gọi là tổng của
chúng.
– Phép nhân (kí hiệu “x” hoặc hai số tự nhiên bất kì cho ta một số tự nhiên duy nhất gọi là tích
của chúng.
2. Tính chất của phép cộng và phép nhân
a) Tính chất giao hoán của phép cộng, phép nhân :
a b = b a;a.b = b.a
Khi đổi chỗ các số hạng trong một tổng thì tổng không đổi.
Khi đổi chỗ các thừa số trong một tích thì tích không đổi.
b) Tính chất kết hợp của phép cộng, phép nhân :
(a b) c = a (b c) ; (a.b).c = a.(b.c)
Muốn cộng một tổng hai số với một số thứ ba, ta có thể cộng số thứ nhất với tổng của số thứ
hai và số thứ ba.
Muốn nhân một tích hai số với một số thứ ba, ta có thể nhân số thứ nhất với tích của số thứ
hai và số thứ ba.
c) Tính chất phân phối của phép nhân đối với phép cộng :
a(b c) = ab ac
Muốn nhân một số với một tổng, ta có thể nhân số đó với từng số hạng của tổng, rồi cộng các
kết quả lại.
d) Cộng với số 0: a 0 = 0 a = a
Tổng của một số với 0 bằng chính số đó.
e) Nhân với số 1: a.1 = 1.a = a
Tích của một số với 1 bằng chính số đó.
Chú ý : Tích của một số với 0 luôn bằng 0.
Nếu tích của hai thừa số mà bằng 0 thì ít nhất một thừa số bằng 0.
B. CÁC DẠNG TOÁN.
Dạng 1: THỰC HÀNH PHÉP CỘNG, PHÉP NHÂN
Phương pháp giải
– Cộng hoặc nhân các số theo “hàng ngang” hoặc theo “cột dọc”;
– Sử dụng máy tính bỏ túi (đối với những bài được phép dùng).
Ví dụ 1. (Bài 26 trang 16 SGK)
Cho các số liệu về quãng đường bộ :
Hà Nội – Vĩnh Yên : 54 km,
Vĩnh Yên – Việt Trì : 19 km, Việt Trì – Yên Bái : 82 km.
Tính qụãng đuờng một ô tô đi từ Hà Nội lên Yên Bái qua Vĩnh Yên và Việt Trì.
Giải
Quãng đường ô tô đi từ Hà Nội lên Yên Bái qua Vĩnh Yên và Việt Trì là :
54 19 82 = 155 (km).
Ví dụ 2. (Bài 28 trang 16 SGK)
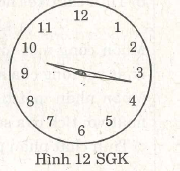
Trên hình 12, đồng hồ chỉ 9 giờ 18 phút, hai kim đồng hồ chia mặt đồng hồ thành hai phần
mỗi phần có sáu số. Tính tổng các số ở mỗi phần, em có nhận xét gì ?
Giải
Tổng các số ở một phần là : 10 11 12 1 2 3 = 39 ;
Tổng các số ở phần kia là: 9 8 7 6 5 4 = 39.
Nhận xét: Tổng các số ở hai phần bằng nhau (đều bằng 39).
Ví dụ 3. (Bài 29 trang 17 SGK)
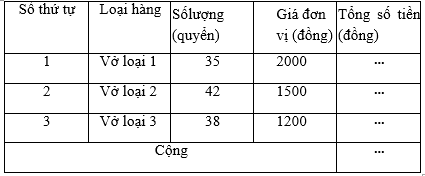
Điền vào chỗ trống trong bảng thanh toán sau :
Giải
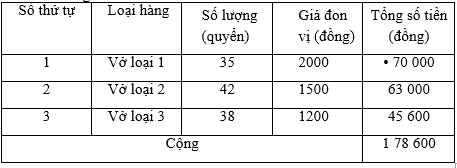
Số tiền mua 35 quyển vở loại 1 là :
2000 . 35 = 70 000 (đ);
Số tiền mua 42 quyển vở loại 2 là :
1500 . 42 = 63 000 (đ);
Số tiền mua 38 quyển vở loại 3 là :
1200 . 38 = 45 600 (đ);
Tổng số tiền mua cả ba loại vở là :
70 000 63 000 45 600 = 178 600 (đ).
Điền vào bảng thanh toán như sau:
Ví dụ 4. (Bài 39 trang 20 SGK)
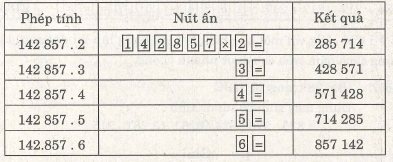
Đố : Số 142857 có tính chất rất đặc biệt. Hãy nhân nó với mỗi số 2, 3, 4, 5, 6 em sẽ tìm được
tính chất đặc biệt ấy.
Giải
142 857 . 2 = 285 714 ; 142 857 . 3 = 428 571 ;
142 857 . 4 = 571 428 ; 142 857 . 5 = 714 285 ;
142 857 . 6 = 857 142.
Nhận xét : số 142 857 nhân với 2, 3, 4, 5, 6 đều được tích là số gồm chính sáu chữ số ấy
viết theo thứ tự khác.
Chú ý : Máy tính SHARP TK – 340 và một số máy tính bỏ túi thông dụng khác cho cách nhân
với một số nhiều lần (thừa số lặp lại đặt trước).
Ví dụ 5. (Bài 33 trang 17 SGK)
Cho dãy số sau : 1 , 1 , 2 , 3 , 5 , 8 , Trong dãy số trên, mỗi số (kể từ số thứ ba) bằng tổng
của hai số liền trước. Hãy viết tiếp bốn số nữa của dãy số.
Giải
Số thứ bảy của dãy là : 5 8 = 13 ;
Số thứ tám của dãy là : 8 13 = 21;
Số thứ chín của dãy là : 13 21 = 34 ;
Số thứ mười của dãy là : 21 34 = 55.
Vậy ta có dãy số: 1, 1 , 2 , 3 , 5 , 8 , 13 , 21 , 34 , 55 , …
Ghi chú : Dãy số nói trên gọi là dãy Phi-bô-na-xi mang tên nhà toán học Italia thế kỉ XIII.
Ví dụ 6. (Bài 34 trang 17 SGK)
Dùng máy tính bỏ túi tính các tổng :
1364 4578 ; 6453 1469 ;
5421 1469 ; 3124 1469 ;
1534 217 217 217.
Giải
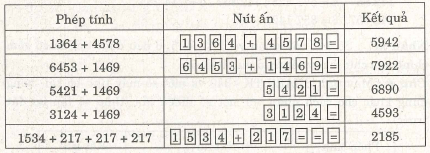
Chú ý : Khi cộng với một số nhiều lần (số hạng lặp lại đặt sau) ta nên áp dụng cách bấm
trên cho được nhanh chóng.
Ví dụ 7. (Bài 38 trang 20 SGK)
Dùng máy tính bỏ túi để tính :
375 . 376 ; 624 . 625 ; 13 . 81. 215.
Giải
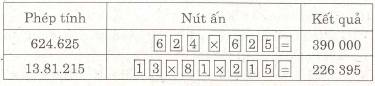
Dạng 2. ÁP DỤNG CÁC TÍNH CHẤT CỦA PHÉP CỘNG VÀ PHÉP NHÂN ĐỂ TÍNH NHANH
Phương pháp giải
– Quan sát, phát hiện các đặc điểm của các số hạng, các thừa số;
– Từ đó, xét xem nên áp dụng tính chất nào (giao hoán, kết hợp, -phân phối) để tính một
cách nhanh chóng.
Ví dụ 8. (Bài 27 trang 16 SGK)
Áp dụng các tính chất của phép cộng và phép nhân để tính nhanh :
a) 86 357 14 ; b) 72 69 128 ;
c) 5.4.27.2 ; d) 28.64 28.36.
Giải
a) 86 357 14 = (86 14) 357 = 100 357 = 457.
b) 72 69 128 = (72 128) 69 = 200 69 = 269.
c) 25.4.27 = (25.4).(5.2).27 = 100.10.27 = 27 000.
d) 64 28.36 = 28.(64 36) = 28.100 = 2800.
Ví dụ 9. (Bài 31 trang 17 SGK)
Tính nhanh :
a) 135 360 65 40 ;
b) 463 318 127 22 ;
c) 20 21 22 … 29 30.
Giải
a) 135 360 65 40 = (135 65) (360 40) = 200 400 = 600.
b) 463 318 127 22 = (463 127) (318 22) = 590 340 = 930.
c) 20 21 22 … 29 30 =
= (20 30) (21 29) (22 28) (23 27) (24 26) 25
= 50.5 25 = 250 25 = 275.
Ví dụ 10. (Bài 32 trang 17 SGK)
Có thể tính nhanh tổng 97 19 bằng cách áp dụng tính chất kết hợp của phép cộng :
97 19 = 97 (3 16) = 07 3) 16 = 100 16 = 116.
Hãy tính nhanh các tổng sau bằng cách làm tương tự như trên :
a) 996 45 ; b) 37 198.
Giải
a) 996 45 = 996 (4 41) = (996 4) 41 = 1000 41 = 1041.
b) 37 198 = (35 2) 198 = 35 (2 198) = 35 200 = 235.
Ví dụ 11. (Bài 35, trang 19 SGK)
Tìm các tích bằng nhau mà không cần tính kết quả của mỗi tích : 15.2.6 ; 4.4.9 ; 5.3.12 ;
8.18 ; 15.3.4 ; 8.2.9.
Giải
15.2.6 = 15.(2.6) = 15.12 ;
5.3.12 = (5.3) .12 = 15.12 ;
15.3.4 = 15.(3.4) = 15.12 .
Vậy: 15.2.6 = 5.3.12 = 15.3.4.
Ta có : 4.4.9 = (4.4),9 = 16.9 ; 8.2.9 = (8.2).9 = 16.9
Suy ra: 4.4.9 = 8.2.9 (1)
Ta lại có : 8.2.9 = 8.(2.9) = 8.18 (2)
Từ (1) và (2) suy ra : 4.4.9 = 8.18 = 8.2.9.
Ví dụ 12. (Bài 36 trang 19 SGK)
Hãy tính nhẩm bằng cách áp dụng tính chất kết hợp của phép nhân: 15.4 ; 25.12 ; 125.16.
Hãy tính nhẩm bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng :
25.12 ; 34.11 ; 47.101
Giải
a) 15.4 = 15.(2.2) = (15.2).2 = 30.2 = 60 ;
= 25.(4.3) = (25.4).3 = 100.3 = 300 ;
= 125.(8.2) = (125.8).2 = 1000.2 = 2000.
b) 25.12 = 25.(10 2) = 25.10 25.2 = 250 50 = 300 ;
34.11 = 34. (10 1) = 34.10 34.1 = 340 34 = 374 ;
47.101 = 47 (100 1) = 47.100 47.1 = 4700 47 = 4747.
Ví dụ 13. (Bài 37 trang 20 SGK)
Áp dụng tính chất a (b – c) = ab – ac để tính nhẩm :
16.19 ; 46.99 ; 35.98.
Giải
16.19 = 16.(20 – 1) = 16.20 – 16.1 = 320 – 16 = 304.
46.99 = 46.(100 – 1) = 46.100 – 46.1 = 4600 – 46 = 4554.
35.98 = 35.(100 – 2) = 35.100 – 35.2 = 3500 – 70 = 3430.
Dạng 3. TÌM SỐ CHƯA BIẾT TRONG MỘT ĐẲNG THỨC
Phương pháp giải
Để tìm số chưa biết trong một phép tính, ta cần nắm vững quan hệ giữa các số trong phép
tính. Chẳng hạn : số bị trừ bằng hiệu cộng với số trừ, một số hạng bằng tổng của hai số
trừ số hạng kia …
Đặc biệt cần chú ý : với mọi a ∈ N ta đều có a.o = 0 , a.1 = a.
Ví dụ 14. (Bài 30 trang 17 SGK)
Tìm x, biết :
a) (x – 34).15 = 0 ; b) 18.(x – 16) = 18.
Giải
Vì (x – 34). 15 = 0 mà 15 ≠ 0 nên x – 34 = 0 . Suy ra x = 34.
(x – 16) = 18 nên x – 16 = 1. Suy ra x = 1 16 = 17.
Ví dụ 15 .
Tìm y, biết :
a) (y – 12) : 5 = 2 ; b) (20 – y).5 = 15.
Giải
a) (y -12) : 5 = 2
y – 12 = 2.5 (số bị chia bằng thương nhân với số chia)
y = 10 12 (số bị trừ bằng hiệu cộng với số trừ)
y = 22
(20 – y).5 = 15
b) 20 – y = 15 : 5 (một thừa số bằng tích chia cho thừa số kia)
y = 20 – 3 (số trừ bằng số bị trừ trừ đi hiệu)
y = 17.
Dạng 4. VIẾT MỘT SỐ DƯỚI DẠNG MỘT TỔNG HOẶC MỘT TÍCH
Phương pháp giải
Căn cứ theo yêu cầu của đề bài, ta có thể viết một số tự nhiên đã cho dưới dạng một tổng
của hai hay nhiều số hạng hoặc dưới dạng một tích của hai hay nhiều thừa số.
Ví dụ 16. Số có hai chữ số 
Theo cách đó, hãy viết số có ba chữ số 
Giải
Trong số
số hàng đơn vị. Do đó, ta có thể viết:
Tương tự như trên, ta có :
Ví dụ 17. Viết số 10 dưới dạng :
a) Tổng của hai số tự nhiên bằng nhau ;
b) Tổng của hai số tự nhiên khác nhau.
Giải
a) 10 = 5 5 ;
b) 10 = 0 10 = l 9 = 2 8
= 3 7 = 4 6 = 10 0 = 9 l
=8 2 = 7 3 = 6 4.
Ví dụ 18. Viết số 16 dưới dạng :
a) Tích của hai số tự nhiên bằng nhau ;
b) Tích của hai số tự nhiên khác nhau.
Giải
a) 16 = 4.4 ; b) 16 = 1.16 = 1 = 2.8 = 8.2.
Ví dụ 19. Tìm hai số tự nhiên a và b biết rằng a.b = 36 và a > 4.
Giải
Số 36 có thể viết dưới dạng tích của hai số tự nhiên như sau :
36 = 1.36 = 2.18 = 3.12 = 4.9 = 6.6 = 36.1 = 18.2 = 12.3 = 9.4.
Vì a > 4 nên a có thể là 6 ; 9 ; 12 ; 18 ; 36.
Ta có bảng các giá trị của và b như sau :
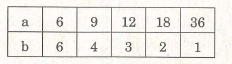
Dạng 5: TÌM CHỮ SỐ CHƯA BIẾT TRONG PHÉP CỘNG, PHÉP NHÂN.
Phương pháp giải
Tính lần lượt theo cột từ phải sang trái. Chú ý những trường hợp có “nhớ”.
Làm tính nhân từ phải sang trái, căn cứ vào những hiểu biết về tính chất của số tự nhiên và
của phép tính, suy luận từng bước để tìm ra những số chưa biết.
Ví dụ 20. Thay dấu * bằng những chữ số thích hợp:
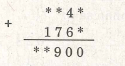
Giải
Ở cột hàng đơn vị, ta có * * được một số tận cùng bằng 0 nhưng ở cột hàng chục 4 6 cũng
tận cùng bằng 0, nghĩa là phép cộng ở hàng đơn vị không có nhớ, do đó * = * = 0.
Ở cột hàng chục 4 6 = 10 viết 0 nhớ 1 sang cột hàng trăm.
Do đó, ở cột hàng trăm : * 7 1 (nhớ) tận cùng bằng 9.
Vậy * = 1.
Ở cột hàng nghìn * 1 được một số có hai chữ số nên * = 9.
Vậy ta có phép cộng sau :
Ví dụ 21. Thay dấu * bằng những chữ số thích hợp:
Giải
Gọi số nhân là
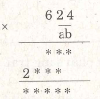
Lần lượt tìm b và a. Ta có :
624.b = * * * do đó b = 1.
624.a = 2 * * * nên a = 4 .
(Vì 624.3 < 2 * * * < 624.5).
Từ đó, ta có phép nhân sau :
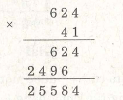
Dạng 6. SO SÁNH HAI TỔNG HOẶC HAI TÍCH MÀ KHÔNG TÍNH CỤ THỂ GIÁ
TRỊ CỦA CHÚNG
Phương pháp giải
Nhận xét, phát hiện và sử dụng các đặc điểm của các số hạng hoặc các thừạ số trong tổng hoặc
tích. Từ đó dựa vào các tính chất của phép cộng và phép nhân để rút ra kết luận.
Ví dụ 22. So sánh hai tổng 1367 5472 và 5377 1462 mà không tính cụ thể giá trị của chúng.
Giải
Ta có : 1367 5472 = (1060 307) (5070 402) =
= (307 5070) (1060 402) = 5377 1462.
Vậy: 1367 5472 = 5377 1462.
Ví dụ 23. So sánh hai tích 2003.2003 và 2002.2004 mà không tính cụ thể giá trị của chúng.
Giải
Nhận xét:
2003.2003 = 2003.(2002 1) = 2003.2002 2003
2002.2004 = 2002.(2003 1) = 2002.2003 2002
So sánh (1) và (2) ta thấy ngay 2003.2003 lớn hơn 2002.2004 một đơn vị.
Dạng 7. TÌM SỐ TỰ NHIÊN CÓ NHIỀU CHỮ SỐ KHI BIẾT ĐIỀU KIỆN XÁC
ĐỊNH CÁC CHỮ SỐ TRONG SỐ ĐÓ
Phương pháp giải
Dựa vào điều kiện xác định các chữ số trong số tự nhiên cần tìm để tìm từng chữ số có
mặt trong số tự nhiên đó.
Ví du 24. (Bài 40 trang 20 SGK)
Bình Ngô đại cáo ra đời năm nào ?
Năm
cuộc kháng chiến do Lê Lợi lãnh đạo chống quân Minh. Biết rằng ab là tổng số ngày
trong hai tuần lễ, còn cd gấp đôi
Tính xem năm $latex overline{abcd} $ là năm nào ?
Giải
Theo đề bài thì
= 28.
Vậy bài Bình Ngô đại cáo ra đời năm