
Định nghĩa:
Căn bậc hai số học của a là số dương x sao cho x2 = a. Ta viết:
$ \displaystyle x=\sqrt{a}\Leftrightarrow \left\{ \begin{array}{l}x\ge 0\\x_{{}}^{2}=a\end{array} \right.$
Hằng đẳng thức: $ \displaystyle \sqrt{A_{{}}^{2}}=\left| A \right|$
Phép toán: A ≥ 0; B ≥ 0
$ \displaystyle \sqrt{A.B}=\sqrt{A}.\sqrt{B}$ (A ≥ 0; B ≥ 0)
$ \displaystyle \sqrt{\frac{A}{B}}=\frac{\sqrt{A}}{\sqrt{B}}$ (A ≥ 0; B > 0)
Phép biến đổi: $ \displaystyle \sqrt{A_{{}}^{2}.B}=\left| A \right|\sqrt{B}$
Phép trục căn ở mẫu: (A ≥ 0; B > 0)
$ \displaystyle \frac{\sqrt{A}}{\sqrt{B}}=\frac{\sqrt{A.B}}{\left| B \right|}$ ;
$ \displaystyle \frac{1}{\sqrt{B}\pm C}=\frac{\sqrt{B}\pm C}{\left| B \right|-C_{{}}^{2}}$ ;
$ \displaystyle \frac{1}{\sqrt{B}\pm \sqrt{C}}=\frac{\sqrt{B}\pm \sqrt{C}}{\left| B \right|-\left| C \right|}$
Căn bậc ba:
1. Khái niệm căn bậc ba:
2. Tính chất
Căn bậc n: (Kiến thức dành cho học sinh khá giỏi, thi vào lớp chuyên Toán)
1. Căn bậc n (2 ≤ n ∈ N) của số a là một số mà lũy thừa n bằng a
2. Căn bậc lẻ (n = 2k + 1)
3. Căn bậc chẵn (n = 2k )
4. Các phép biến đổi căn thức:
Bài: Tính
$ \displaystyle A=3\sqrt{75}+\sqrt{192}-5\sqrt{108}-\frac{2}{3}\sqrt{243}$
= $ \displaystyle 3\sqrt{25.3}+\sqrt{64.3}-5\sqrt{36.3}-\frac{2}{3}\sqrt{81.3}$
= $ \displaystyle 3\sqrt{5_{{}}^{2}.3}+\sqrt{8_{{}}^{2}.3}-5\sqrt{6_{{}}^{2}.3}-\frac{2}{3}\sqrt{9_{{}}^{2}.3}$
= $ \displaystyle 15\sqrt{3}+8\sqrt{3}-5.6\sqrt{3}-\frac{2}{3}.9\sqrt{3}$
= $ \displaystyle -13\sqrt{3}$
Nhận xét: Phân tích và áp dụng Phép biến đổi $ \displaystyle \sqrt{A_{{}}^{2}.B}=\left| A \right|\sqrt{B}$
Bài tập rèn luyện
$ \displaystyle B=6\sqrt{80}+5\sqrt{45}+4\sqrt{1.25}-5\sqrt{\frac{1}{5}}$ ;
$ \displaystyle C=\sqrt{7}-\frac{1}{2}\sqrt{28}-20\sqrt{0.07}+\frac{1}{5}\sqrt{175}$
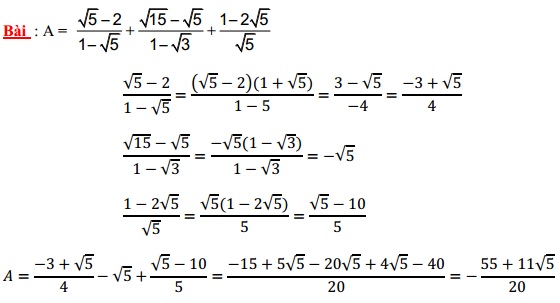
Nhận xét:
– Ta trục căn từng phân thức sau đó ghép lại.
– Trước khi trục căn ở mẫu, ta rút gọn phân thức.
Bài tập rèn luyện
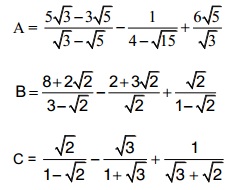
Phương pháp giải:
– Áp dụng công thức: (A ± B)2 = A2 ± 2AB + B2
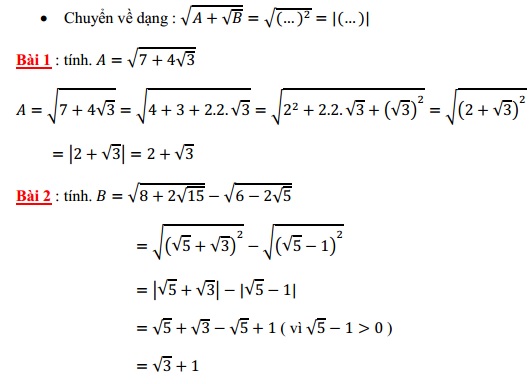
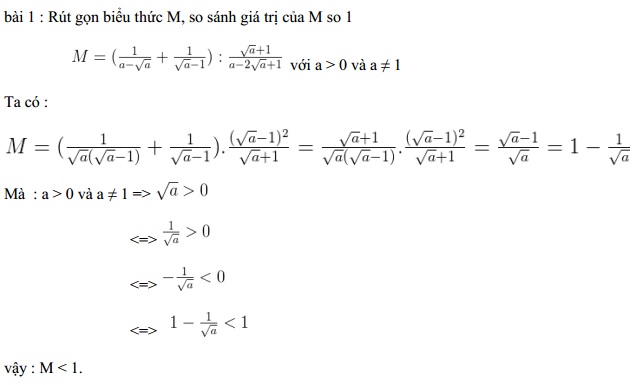
Bài tập rèn luyện
$ \displaystyle A=\left( \frac{1}{a-\sqrt{a}}+\frac{\sqrt{a}}{a-1} \right):\frac{a\sqrt{a}-1}{a\sqrt{a}-2a+\sqrt{a}}$ (a > 0 và a ≠ 1)
Phương pháp giải:
Định nghĩa:
$ \displaystyle x=\sqrt{a}\Leftrightarrow \left\{ \begin{array}{l}x\ge 0\\x_{{}}^{2}=a\end{array} \right.$ ;
Công thức:
$ \displaystyle \sqrt{A}=B\Leftrightarrow \left\{ \begin{array}{l}B\ge 0\\A=B_{{}}^{2}\end{array} \right.$ ;
$ \displaystyle \sqrt{A}=\sqrt{B}\Leftrightarrow \left\{ \begin{array}{l}A\ge 0;B\ge 0\\A=B\end{array} \right.$
Giải bài tập mẫu:
Bài: Tìm x. biết:
Ta có : 5 ≥ 0, nên : x – 3 = 52 = 25
<=> x = 25 + 3
<=> x = 28
Vậy : x = 28
Bài tập rèn luyện
a) $ \displaystyle \sqrt{36x}-\sqrt{25x}=2$
b) $ \displaystyle \sqrt{x_{{}}^{2}+6x+9}+1-2x=0$
c) $ \displaystyle \sqrt{x-1+2\sqrt{x-2}}+\sqrt{x+7+6\sqrt{x-2}}=8$