
Bài I (2,0 điểm). Với $ x\ge 0,x\ne 9$, cho hai biểu thức:
A = $ \frac{7}{{\sqrt{x}+8}}$ và B = $ \frac{{\sqrt{x}}}{{\sqrt{x}-3}}+\frac{2}{{\sqrt{x}+3}}-\frac{{18}}{{x-9}}$
1) Tính giá trị của A khi x = 36
2) Chứng minh B = $ \frac{{\sqrt{x}+8}}{{\sqrt{x}+3}}$
3) Tìm tất cả giá trị của x để biểu thức P = A.B có giá trị là số nguyên.
Bài II (2,0 điểm). Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một ô tô và một xe máy cùng khởi hành từ A để đi đến B. Biết rằng quãng đường AB dài 60km và vận tốc của mỗi xe không đổi trên toàn bộ quãng đường. Do vận tốc xe ô tô lớn hơn vận tốc xe máy là 15km/giờ nên ô tô đến B sớm hơn xe máy 40 phút. Tìm vận tốc của mỗi xe.
Bài III (2,0 điểm).
1) Giải hệ phương trình: $ \left\{ \begin{array}{l}\frac{{2x}}{{x-1}}+\sqrt{{y+1}}=7\\\frac{{3x}}{{x-1}}-2\sqrt{{y+1}}=0\end{array} \right.$
1) Cho parabol (P): $ y=\frac{1}{2}{{x}^{2}}$ và đường thẳng (d): $ y=2mx+4$ trong mặt phẳng tọa độ Oxy.
a) Chứng minh (d) luôn cắt (P) tại hai điểm phân biệt với mọi giá trị của m.
b) Gọi $ {{x}_{1}},{{x}_{2}}$ là hoành độ các giao điểm của (d) và (P). Tìm số dương m để $ |{{x}_{1}}|+2|{{x}_{2}}|=8$
Bài IV (3,5 điểm).
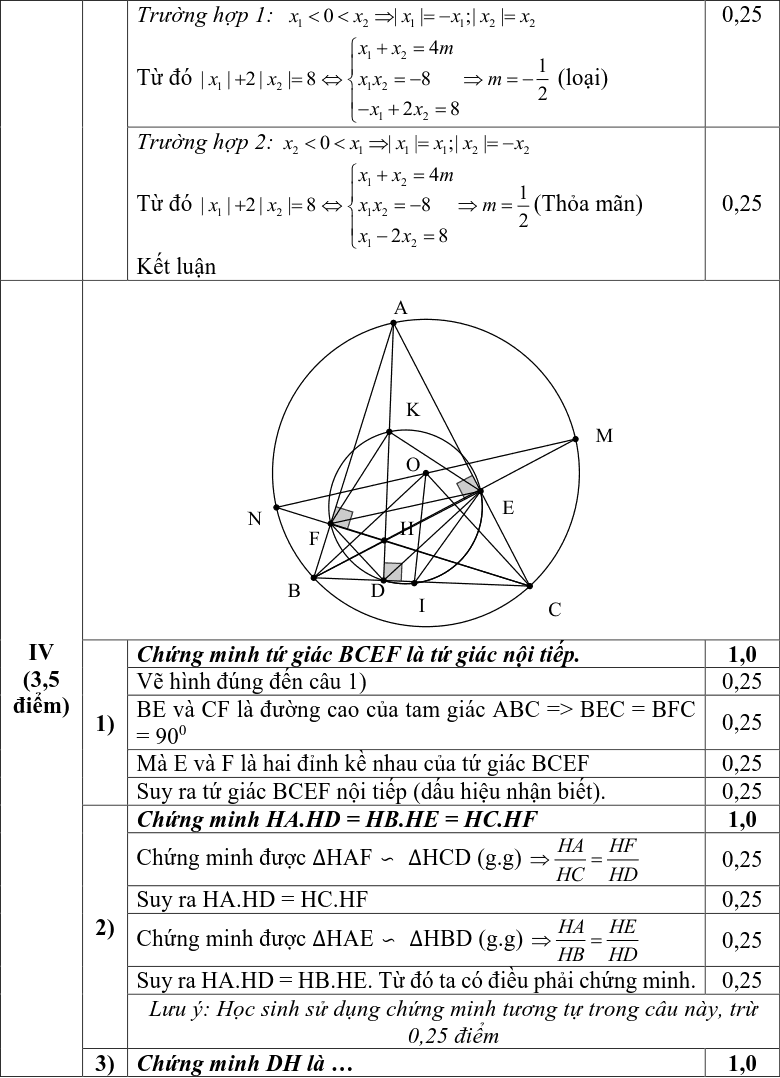
Cho tam giác ABC nhọn, nội tiếp đường tròn (O). Ba đường cao AD, BE, CF của tam giác ABC cùng đi qua trực tâm H.
1) Chứng minh tứ giác BCEF là tứ giác nội tiếp.
2) Chứng minh HA.HD = HB.HE = HC.HF
3) Đường tròn ngoại tiếp tam giác DEF cắt cạnh BC tại giao điểm thứ hai là I. Chứng minh DH là tia phân giác của góc EDF và I là trung điểm của BC.
4) Hai tia BE, CF cắt (O) tại các giao điểm thứ hai lần lượt là M và N. Chứng minh nếu $ \frac{{MN}}{{OI}}=2\sqrt{2}$ thì MN là đường kính của (O).
Bài V (0,5 điểm).
Cho a, b, c là các số không âm thỏa mãn $ {{a}^{2}}+{{b}^{2}}+{{c}^{2}}=3$. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = $ ab+bc+ca-abc$
—HẾT—
Ghi chú:
Học sinh không sử dụng tài liệu, không trao đổi khi làm bài.
Giáo viên làm nhiệm vụ coi khi không giải thích gì thêm.



Cán bộ chấm thi lưu ý:
– Điểm toàn bài để lẻ đến 0,25
– Các câu hoặc các ý có cách làm khác với hướng dẫn ở trên nếu đúng vẫn được điểm tối đa của câu hay ý đó.
– Bài IV: Thí sinh vẽ sai hình trong phạm vi câu nào thì không tính điểm câu đó.