
KỲ THI HSG CẤP HUYỆN NĂM HỌC 2016-2017
Khóa ngày: 26/10/2016
Môn: GTBMT cầm tay Casio – Lớp 9
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Bài 1 (5,0 điểm). Tính giá trị các biểu thức sau: (chỉ ghi kết quả)
a. Tính giá trị của biểu thức:
$ \displaystyle A=\frac{{{2}^{98}}+{{2}^{97}}+{{2}^{96}}+…+2+1}{{{2}^{32}}+{{2}^{31}}+{{2}^{30}}+…+2+1}$
b) $ \displaystyle B=\frac{1}{\sqrt{1}+\sqrt{5}}+\frac{1}{\sqrt{2}+\sqrt{6}}+…+\frac{1}{\sqrt{2012}+\sqrt{2016}}+\frac{1}{\sqrt{2013}+\sqrt{2017}}$
|
a) Kết quả: A =…………………………….. |
|
b) Kết quả: B = ……………………… |
Bài 2 (5,0 điểm) (chỉ ghi kết quả)
a) Tìm x biết:
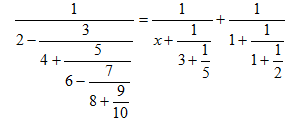
b) Tính: (kết quả lấy 4 chữ số thập phân).
$ \displaystyle P=\frac{{{\sin }^{3}}{{90}^{0}}-{{\cot }^{3}}{{30}^{0}}-{{\cos }^{2}}{{45}^{0}}+\tan {{20}^{0}}}{2\sqrt[{}]{7}+\sin {{108}^{0}}\cos {{32}^{0}}\tan {{64}^{0}}}$
| a) Kết quả: x = …………………..…. |
| b) Kết quả: P ……………..………… |
Bài 3 (5,0 điểm).
Khi chia đa thức $ \displaystyle P(x)={{x}^{81}}+a{{x}^{57}}+b{{x}^{41}}+c{{x}^{19}}+2x+1$ cho (x –1) được số dư là 5 và khi chia đa thức P(x) cho ( x – 2) được số dư là – 4 .
a) Hãy tìm các số thực A, B biết đa thức $ \displaystyle Q(x)={{x}^{81}}+a{{x}^{57}}+b{{x}^{41}}+c{{x}^{19}}+Ax+B$ chia hết cho đa thức x2 – 3x + 2
b) Với giá trị của A và B vừa tìm được, hãy tính giá trị của đa thức
$ \displaystyle R(x)=Q(x)-P(x)+{{x}^{81}}+{{x}^{57}}-2{{x}^{41}}+2{{x}^{19}}+2x+1$
tại x = 1,032016
| Sơ lược cách giải:
…………………………………………………………………………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..……………………………………………………………………………………………………. …………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..……………………………… |
|
Kết quả: A = …………..; B= ……………..
|
b)
|
Kết quả: R(1,032016) » ……………………………………………….………………. |
Bài 4 (5,0 điểm).
Tìm tất cả các cặp số nguyên (x, y) thỏa mãn: 10x + y = x2 + y2 + 1
| Sơ lược cách giải:
…………………………………………………………………………………………..…………………………………………………………………………………………..……………………………………………………………………………………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..…………………………………………………………………………………………..………………………………………………………………………………… |
| Kết quả: (x;y) = …………………………………………………………………. |
Bài 5 (5,0 điểm).
Cho tam giác ABC vuông tại A, đường cao AH , có AB= 3,5cm; AC = 4,5cm.
a) Tính BC, AH, BH.
b) Kẻ phân giác của góc A cắt BC tại I. Tính BI, CI
| Hình vẽ và tóm tắt cách giải | Kết quả |
| Hình vẽ:
|
a) Kết quả
BC ≈ BH ≈ CH ≈
b) Kết quả BI ≈. CI ≈ |
Bài 6 (5điểm).
Cho tam giác ABC có AB = 13.2cm, AC = $ \sqrt{583.0884}$ , trung tuyến AM=10.11cm. Tính diện tích tam giác ABC.(Kết quả làm tròn đến 3 chữ số thập phân)
Bài 7 (5,0 điểm).
Cho tam giác đều ABC có cạnh a = 1,2345m. M thuộc cạnh BC sao cho $ \displaystyle AM=\frac{a\sqrt{14}}{4}$ . Gọi N và P là các điểm lần lượt thuộc AC, AB. Tìm giá trị nhỏ nhất của chu vi tam giác MNP (kết quả lấy 5 chữ số thập phân)
Bài 8 (5,0 điểm).
Cho dãy số a1 = 3, a2 = 4, a3 = 6,….., an+1 = an + n
a) Tính : a5 , a6, a7 , a8, a9.
b) Xác định số thứ 20162017 của dãy số trên .
Bài 9 (10 điểm).
Quãng đường AB dài 10,15km, một người đi bộ xuất phát từ A và một người đi xe đạp xuất phát từ B, hai người xuất phát cùng lúc và đi về phía nhau. Cùng thời điểm đó, 1 người đi xe máy từ A đến B. Khi gặp người đi xe đạp từ B đến, người đi xe máy lập tức quay về phía A, khi gặp người đi bộ từ A, lại quay về phía B…. Cứ thế cho tới khi cả 3 người gặp nhau.
Biết vận tốc người đi bộ là 5,15km/h, vận tốc người đi xe đạp 15,16km/h, vận tốc người đi xe máy là 45,17 km/h.
a) Tính quãng đường người đi xe máy đi được khi 3 người gặp nhau (làm tròn đến mét).
b) Chỗ gặp nhau của 3 người cách A bao nhiêu kilômét (làm tròn 4 chữ số thập phân).