Bài 1 (2 điểm). Cho hai biểu thức
A = $ (\frac{{\sqrt{x}}}{{\sqrt{x}-1}}+\frac{1}{{x-\sqrt{x}}}):\left( {\frac{1}{{\sqrt{x}+1}}+\frac{2}{{x-1}}} \right)$ với x >0; x ≠ 1
1) Rút gọn biểu thức A
2) Tìm x biết A=2
3) Tìm giá trị nhỏ nhất của biểu thức $ P=(A-4)\sqrt{x}$
Bài 2 (2 điểm). Giải toán bằng cách lập phương trình hoặc hệ phương trình
Một ô tô đi từ A đến B cách nhau 90km với vận tốc dự định. Khi từ B trở về A, ô tô đi với vận tốc nhanh hơn vận tốc lúc đi là 5km/ giờ. Do đó thời gian về ít hơn thời gian đi là 15 phút. Tính vận tốc dự định của ô tô đi từ A đến B.
Bài 3 (2.5 điểm).
1) Giải hệ phương trình: $ \left\{ \begin{array}{l}\sqrt{{x-2}}+2(x-y)=8\\2\sqrt{{x-2}}+5(x-y)=19\end{array} \right.$
2) Trong mặt phẳng tọa độ Oxy cho đường thẳng (d): y=mx-m-2 ( m là tham số) và parabol (P): y=-x2.
a) với m = -2. Tìm tọa độ giao điểm của đường thẳng d và parabol (P).
b) tìm m để đường thẳng (d) cắt parabol (P) tại 2 điểm phân biệt có hoành độ x1, x2 thỏa mãn $ \left| {{{x}_{1}}-{{x}_{2}}} \right|=\sqrt{{20}}$
Bài 4 (3 điểm)
1) Một hộp sữa hình trụ có đường kính đáy là 12cm, chiều cao 10cm. Tính diện tích vật liệu dùng để tạo nên một vỏ hộp như vậy (không tính phần mép nối)
2) Cho đường tròn (O,R), từ điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB,AC với (O) ( B,C lần lượt là các tiếp điểm).
a) Chứng minh tứ giác ABOC là tứ giác nội tiếp
b) Gọi D là trung điểm của AC, BD cắt đường tròn tại E, đường thẳng AE cắt đường tròn (O) tại điểm thứ hai là F. chứng minh AB2 = AE. AF.
c) Chứng minh BC=CF.
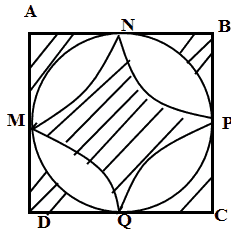
Bài 5 (0,5 điểm). Một viên gạch hinhg vuông cạnh a(cm) có hoa văn như hình vẽ. M,N,P,Q lần lượt là trung điểm của các cạnh AD,AB,BC,CD.
Tìm độ dài a biết diện tích phần gạch chéo là $ 200(4-\pi )(c{{m}^{2}})$.