Bài I (2 điểm). Giải các phương trình, hệ phương trình sau:
1) 3x2 – 14x + 8 = 0
2) $ \left\{ \begin{array}{l}\frac{1}{{x-1}}+\frac{1}{y}=-1\\\frac{3}{{x-1}}-\frac{2}{y}=7\end{array} \right.$
Bài II (2 điểm). Giải bài toán bằng cách lập phương trình hoặc hệ phương trình:
Một ca nô chạy xuôi dòng trên một khúc sông dài 132km, sau đó chạy ngược dòng 104km trên khúc sông đó. Tính vận tốc của ca nô khi nước yên lặng, biết rằng vận tốc của dòng nước là 4km/h và thời gian ca nô chạy xuôi dòng ít hơn thời gian chạy ngược dòng là 1 giờ.
Bài III (2 điểm). Cho phương trình: x2 – 2mx – 4 = 0 (x là ẩn; m là tham số) (1)
1) Chứng minh rằng phương trình (1) luôn có 2 nghiệm phân biệt với mọi m.
2) Tìm m để phương trình (1) có 2 nghiệm x1 và x2 thỏa mãn: x12 + x22 = – 3x1x2.
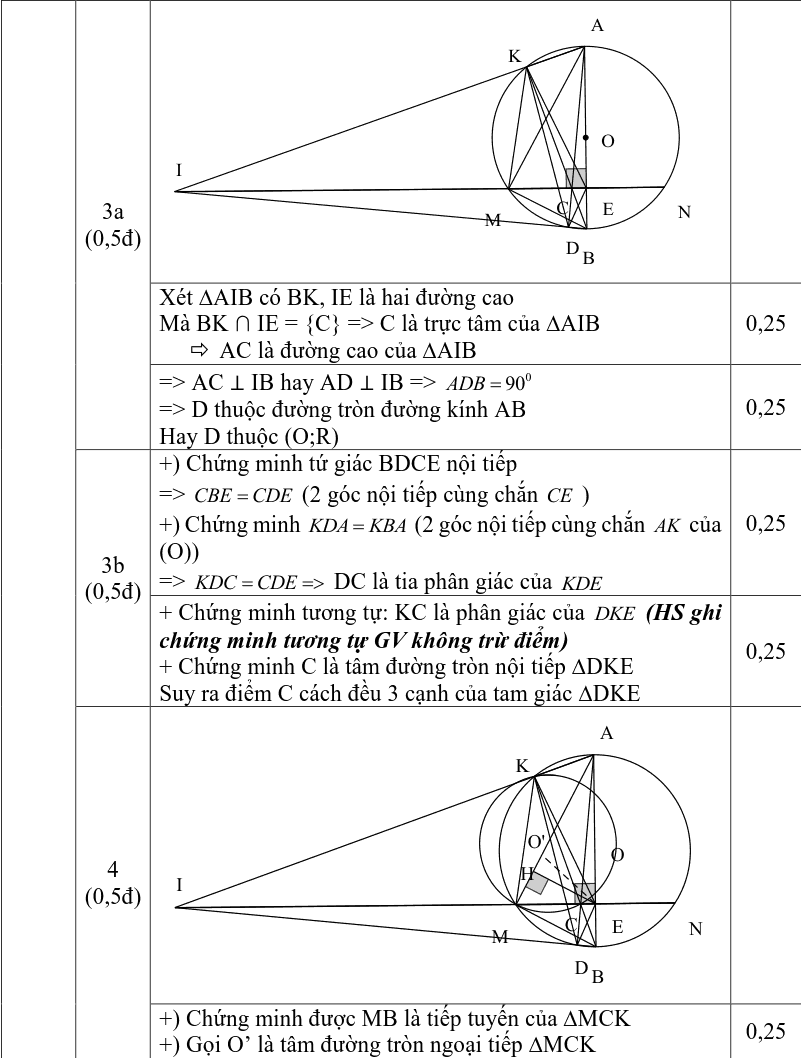
Bài IV (3,5 điểm). Cho đường tròn (O;R), dây MN cố định (MN < 2R). Kẻ đường kính AB vuông góc với dây MN tại E. Lấy điểm C thuộc dây MN (C khác M, N, E), BC cắt đường tròn (O) tại điểm K (K khác B).
1)Chứng minh: Tứ giác AKCE nội tiếp được một đường tròn.
2) Chứng minh: BM2 = BK.BC
3) Gọi I là giao điểm của AK và MN; D là giao điểm của AC và BI
a) Chứng minh: D thuộc (O;R)
b) Chứng minh điểm C cách đều ba cạnh của ∆DEK
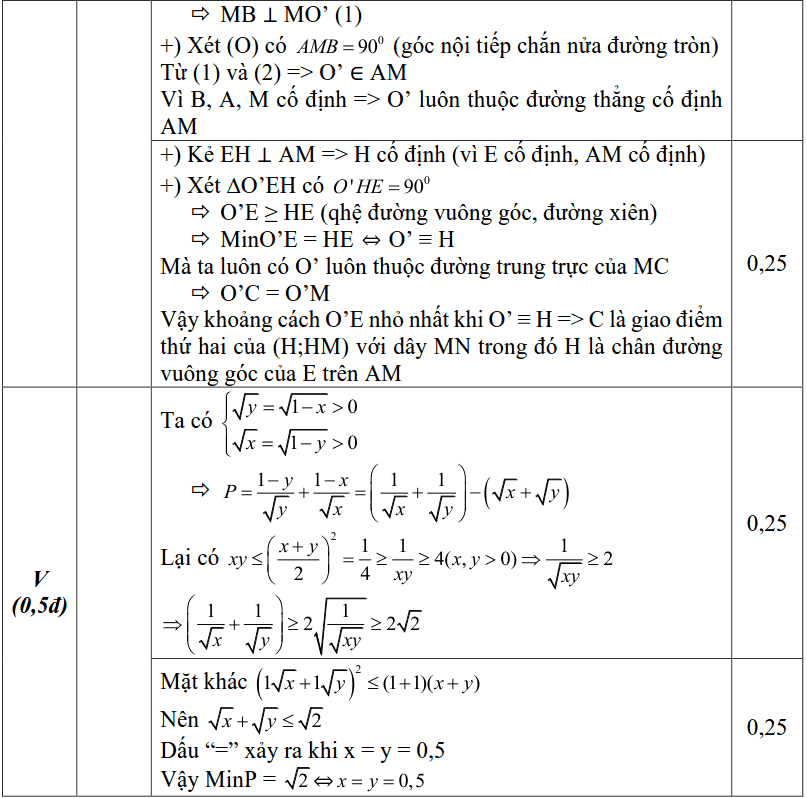
4) Xác định vị trí điểm C trên dây MN để khoảng cách từ E đến tâm đường tròn ngoại tiếp ∆MCK nhỏ nhất.
Bài V (0,5 điểm). Cho x, y dương thỏa mãn x + y = 1. Tìm giá trị nhỏ nhất của biết P = $ \frac{x}{{\sqrt{{1-x}}}}+\frac{y}{{\sqrt{{1-y}}}}$
A. Hướng dẫn chung
– Nếu học sinh giải theo cách khác mà đúng và đủ các bước thì giám khảo vẫn cho điểm tối đa.
– Trong mỗi bài, nếu ở một bước nào đó bị sai thì các bước sau có liên quan không được điểm.
– Bài hình học bắt buộc phải vẽ đúng hình thì mới chấm điểm, nếu không có hình vẽ đúng ở phần nào thì giám khảo không cho điểm phần lời giải liên quan đến hình của phần đó.
– Điểm toàn bài là tổng điểm của các ý, các câu, tính đến 0,25 điểm và không làm tròn.
B. Đáp án và thang điểm