

Câu 1 (2 điểm)
a) Tính nhanh: 16 + (27 – 7.6) – (94.7 – 27. 99)
b) Tính tổng: A =
Câu 2 (2 điểm) Cho biểu thức: M = 5 + 52 + 53 + … + 580. Chứng tỏ rằng:
a) M chia hết cho 6.
b) M không phải là số chính phương.
Câu 3 (2 điểm)
a) Chứng tỏ rằng: $ \displaystyle \frac{2n+5}{n+3},\left( n\in N \right)$ là phân số tối giản.
b) Tìm các giá trị nguyên của n để phân số B = $ \displaystyle \frac{2n+5}{n+3}$ có giá trị là số nguyên.
Câu 4 (1 điểm) Tìm số tự nhiên nhỏ nhất sao cho khi chia số đó cho 3 dư 1; chia cho 4 dư 2; chia cho 5 dư 3; chia cho 6 dư 4 và chia hết cho 11.
Câu 5 (2 điểm) Trên cùng nửa mặt phẳng bờ chứa tia Ox vẽ 3 tia Oy, Oz, Ot sao cho $ \displaystyle \widehat{xOy}={{30}^{\circ }};\widehat{xOz}={{70}^{\circ }};\widehat{xOt}={{110}^{\circ }}$
a) Tính $ \displaystyle \widehat{yOz}$ và $ \displaystyle \widehat{zOt}$
b) Trong 3 tia Oy, Oz, Ot tia nào nằm giữa 2 tia còn lại? Vì sao?
c) Chứng minh: Oz là tia phân giác của góc yOt.
Câu 6 (1 điểm) Chứng minh rằng: $ \displaystyle \frac{1}{{{2}^{2}}}+\frac{1}{{{3}^{2}}}+\frac{1}{{{4}^{2}}}+…+\frac{1}{{{100}^{2}}}<1$
Đáp án:
Câu 1 (Mỗi câu đúng, cho 1 điểm)
a) 16 + (27 – 7.6) – (94.7 – 27. 99)
= 16 + 27 – 7.6 – 94.7 + 27.99
= 16 + 27 + 27.99 – 7.6 – 94.7
= 16 + 27(99 + 1) – 7.(6 + 94)
= 16 +27.100 – 7. 100
= 16 + 100(27- 7) = 16 + 100.20 = 16 + 2000 = 2016
b) A = $ \frac{2}{{1.4}}+\frac{2}{{4.7}}+\frac{2}{{7.10}}+….+\frac{2}{{97.100}}$
Ta có $ \frac{1}{{1.4}}=\frac{1}{3}(\frac{1}{1}-\frac{1}{4})\Rightarrow \frac{2}{{1.4}}=\frac{2}{3}(\frac{1}{1}-\frac{1}{4})$
Tương tự: $ \displaystyle \frac{2}{{4.7}}=\frac{2}{3}(\frac{1}{4}-\frac{1}{7});\frac{2}{{7.10}}=\frac{2}{3}(\frac{1}{7}-\frac{1}{{10}})$; ……; $ \frac{2}{{97.100}}=\frac{2}{3}(\frac{1}{{99}}-\frac{1}{{100}})$
⇒ A = $ \frac{2}{3}(\frac{1}{1}-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{{10}}+…..+\frac{1}{{99}}-\frac{1}{{100}})$ = $ \frac{2}{3}(\frac{1}{1}-\frac{1}{{100}})=\frac{2}{3}.\frac{{99}}{{100}}=\frac{{33}}{{50}}$
Câu 2 (Mỗi câu đúng, cho 1 điểm)
a) Ta có: M = 5 + 52 + 53 + … + 580
= 5 + 52 + 53 + … + 580 = (5 + 52) + (53 + 54) + (55 + 56) +… + (579 + 580)
= (5 + 52) + 52.(5 + 52) + 54(5 + 52) + … + 578(5 + 52)
= 30 + 30.52 + 30.54 + … + 30.578 = 30 (1+ 52 + 54 + … + 578) $ \displaystyle \vdots $ 30
b) Ta thấy : M = 5 + 52 + 53 + … + 580 chia hết cho số nguyên tố 5.
Mặt khác, do: 52+ 53 + … + 580 chia hết cho 52 (vì tất cả các số hạng đều chia hết cho 52)
⇒ M = 5 + 52 + 53 + … + 580 không chia hết cho 52 (do 5 không chia hết cho 52)
⇒ M chia hết cho 5 nhưng không chia hết cho 52
⇒ M không phải là số chính phương.
(Vì số chính phương chia hết cho số nguyên tố p thì chia hết cho p2).
Câu 3 (Mỗi câu đúng, cho 1 điểm)
a) Chứng tỏ rằng: $ \displaystyle \frac{{2n+5}}{{n+3}},\left( {n\in N} \right)$ là phân số tối giản.
Gọi d là ước chung của n + 3 và 2n + 5 với d ∈ N
⇒ n + 3 $ \vdots $ d và 2n + 5 $ \vdots $ d
⇒ (n + 3) – (2n + 5) $ \vdots $ d Þ 2(n + 3) – (2n + 5) $ \vdots $ d ⇔ 1 $ \vdots $ d ⇒ d = 1 ∈ N
⇒ ƯC( n + 3 và 2n + 5) = 1
⇒ ƯCLN (n + 3 và 2n + 5) = 1 ⇒ $ \displaystyle \frac{{2n+5}}{{n+3}},\left( {n\in N} \right)$ là phân số tối giản.
b) Tìm các giá trị nguyên của n để phân số B = $ \displaystyle \frac{{2n+5}}{{n+3}}$ có giá trị là số nguyên.
Ta có: $ \displaystyle \frac{{2n+5}}{{n+3}}$ = $ \displaystyle \frac{{2(n+3)-1}}{{n+3}}$ = 2 – $ \displaystyle \frac{1}{{n+3}}$
Để B có giá trị nguyên thì $ \displaystyle \frac{1}{{n+3}}$ nguyên.
Mà $ \displaystyle \frac{1}{{n+3}}$ nguyên ⇔ 1 $ \vdots $(n +3) hay n +3 là ước của 1.
Do Ư(1) = {±1}; Ta tìm được n = {-4 ; – 2}
Câu 4: Giải
Gọi số phải tìm là x.
Theo bài ra ta có x + 2 chia hết cho 3, 4, 5, 6.
⇒ x + 2 là bội chung của 3, 4, 5, 6
Mà BCNN(3; 4; 5; 6) = 60 nên x + 2 = 60.n .
Do đó x = 60.n – 2 ; (n = 1; 2; 3…..)
Mặt khác x$ \vdots $11 nên lần lượt cho n = 1; 2; 3…. Ta thấy n = 7 thì x = 418 $ \vdots $11
Vậy số nhỏ nhất phải tìm là 418.
Câu 5 (Vẽ hình đúng, cho 0,5 điểm. Còn lại mỗi ý 0,5 điểm)
a) $ \displaystyle \widehat{{xOy}}<\widehat{{xOz}}$ (300 < 700)
⇒ Tia Oy nằm giữa 2 tia Ox và Oz
⇒ $ \displaystyle \widehat{{yOz}}$ = 700 – 300 = 400
$ \displaystyle \widehat{{xOz}}<\widehat{{xOt}}$ (700 < 1100)
⇒ Tia Oz nằm giữa 2 tia Ox và Ot
⇒ $ \displaystyle \widehat{{zOt}}$ = 1100 – 700 = 400
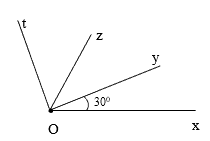
b) $ \displaystyle \widehat{{xOy}}<\widehat{{xOt}}$ (300 < 1100)
⇒ Tia Oy nằm giữa 2 tia Ox và Ot
⇒ $ \displaystyle \widehat{{yOt}}$ = 1100 – 300 = 800
Theo trên, $ \displaystyle \widehat{{yOz}}$ = 400
⇒ $ \displaystyle \widehat{{yOz}}$ < $ \displaystyle \widehat{{yOt}}$ (400 < 800)
⇒ Tia Oz nằm giữa 2 tia Oy và Ot
c) Theo trên:
Tia Oz nằm giữa 2 tia Oy và Ot và có:
$ \displaystyle \widehat{{yOz}}$ = 400; $ \displaystyle \widehat{{zOt}}$ = 400
⇒ Oz là tia phân giác của góc yOt.
Câu 6 Chứng minh rằng : $ \frac{1}{{{{2}^{2}}}}$+$ \frac{1}{{{{3}^{2}}}}$+$ \frac{1}{{{{4}^{2}}}}$+…+$ \frac{1}{{{{{100}}^{2}}}}$< 1
Ta có $ \frac{1}{{{{2}^{2}}}}$<$ \frac{1}{{2.1}}$=$ \frac{1}{1}$-$ \frac{1}{2}$
$ \frac{1}{{{{3}^{2}}}}$<$ \frac{1}{{2.3}}$=$ \frac{1}{2}$-$ \frac{1}{3}$
..
$ \frac{1}{{{{{100}}^{2}}}}$<$ \frac{1}{{99.100}}$=$ \frac{1}{{99}}$-$ \frac{1}{{100}}$
⇒ $ \frac{1}{{{{2}^{2}}}}$+$ \frac{1}{{{{3}^{2}}}}$+…+ $ \frac{1}{{{{{100}}^{2}}}}$<$ \frac{1}{1}$-$ \frac{1}{2}$+$ \frac{1}{2}$-$ \frac{1}{3}$+ …+$ \frac{1}{{99}}$-$ \frac{1}{{100}}$ = 1-$ \frac{1}{{100}}$ <1
Chú ý: Nếu học sinh làm theo cách khác đúng, vẫn cho điểm tối đa.