PHẦN I. TRẮC NGHIỆM(2 điểm)
(Thí sinh không cần giải thích và không phải chép lại đề bài, hãy viết kết quả các bài toán sau vào tờ giấy thi)
1. Biểu thức A = $ \displaystyle \sqrt{2x+1}$ có nghĩa với các giá trị của x là…
2. Giá trị m để 2 đường thẳng (d1): y = 3x – 2 và (d2): y = mx + 3m – 1 cắt nhau tại 1 điểm trên trục tung là….
3. Các nghiệm của phương trình $ \displaystyle \left| 3x-5 \right|=1$ là…
4. Giá trị của m để phương trình x2 – (m+1)x – 2 = 0 có 2 nghiệm x1, x2 thỏa mãn x12x2 + x1x22 = 4 là…
PHẦN II. TỰ LUẬN (8 điểm)
Bài 1. (2 điểm)
a) Giải hệ phương trình $ \displaystyle \left\{ \begin{array}{l}\frac{1}{x}+\frac{1}{y}=5\\\frac{2}{x}-\frac{3}{y}=-5\end{array} \right.$
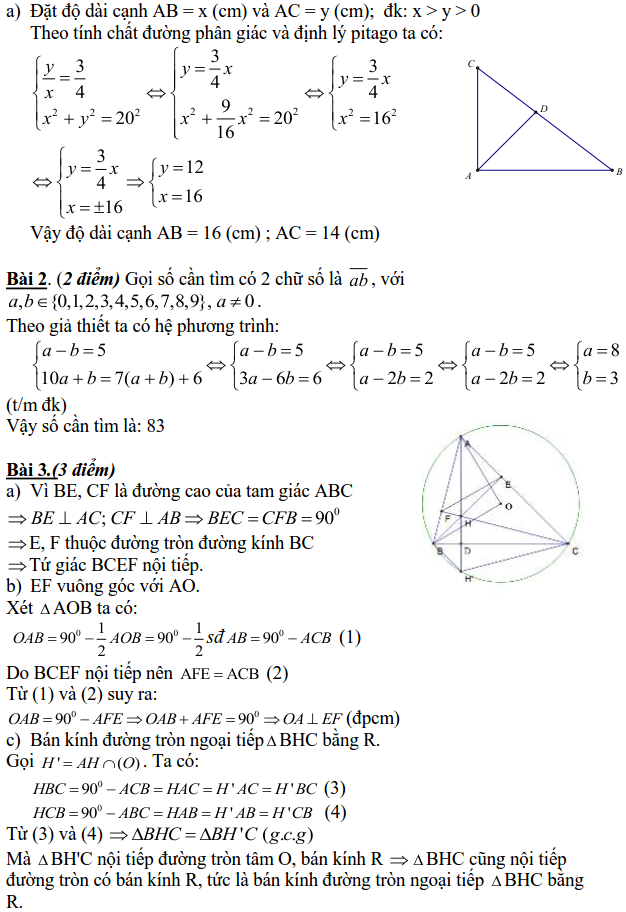
b) Cho tam giác ABC vuông tại A (AB > AC). Đường phân giác AD chia cạnh huyền BC thành 2 đoạn theo tỷ lệ $ \displaystyle \frac{3}{4}$ và BC = 20cm. Tính độ dài hai cạnh góc vuông.
Bài 2. (2 điểm) Tìm một số có hai chữ số, biết rằng chữ số hàng chục lớn hơn chữ số hàng đơn vị là 5 và nếu đem số đó chia cho tổng các chữ số của nó thì được thương là 7 và dư là 6.
Bài 3.(3 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp trong đường tròn tâm O, bán kính R. Các đường cao AD, BE, CF của tám giác cắt nhau tại H. Chứng minh rằng:
a) Tứ giác BCEF nội tiếp được.
b) EF vuông góc với AO.
c) Bán kính đường tròn ngoại tiếp tam giác BHC bằng R.
Bài 4. (1 điểm) Trên các cạnh của một hình chữ nhật đặt lần lượt 4 điểm tùy ý. Bốn điểm này tạo thành một tứ giác có độ dài các cạnh lần lượt là x, y, z , t. Chứng minh rằng
25 x2 + y2 + z2 + t2 ≤ 50. Biết rằng hình chữ nhật có chiều dài và chiều rộng là 4 và 3.
ĐÁP ÁN
PHẦN I. TRẮC NGHIỆM(2 điểm)
1. Biểu thức A = $ \displaystyle \sqrt{2x+1}$ có nghĩa với các giá trị của x là: $ x\ge -\frac{1}{2}$
2. Giá trị m để 2 đường thẳng (d1): y = 3x – 2 và (d2): y = mx + 3m – 1 cắt nhau tại 1 điểm trên trục tung là $ m=-\frac{1}{3}$.
3. Các nghiệm của phương trình $ \displaystyle \left| 3x-5 \right|=1$ là: x = 2; x = $ \frac{4}{3}$.
4. Giá trị của m để phương trình x2 – (m+1)x – 2 = 0 có 2 nghiệm x1, x2 thỏa mãn x12x2 + x1x22 = 4 là m = -3.
PHẦN II. TỰ LUẬN(8 điểm)
Bài 1. (2 điểm)
a) Giải hệ phương trình: $ \displaystyle \left\{ \begin{array}{l}\frac{1}{x}+\frac{1}{y}=5\,\,\,\,\,\,\,\,(1)\\\frac{2}{x}-\frac{3}{y}=-5\,\,\,\,(2)\end{array} \right.$
Điều kiện: $ x,y\ne 0.$
Lấy (1) cộng (2) theo vế, ta được: $ \displaystyle \frac{3}{x}-\frac{2}{y}=0\Leftrightarrow 3y=2x\Leftrightarrow y=\frac{2x}{3}$, thế vào (1) ta có pt:
$ \displaystyle \frac{1}{x}+\frac{3}{2x}=5\Leftrightarrow \frac{5}{2x}=5\Leftrightarrow 2x=1\Leftrightarrow x=\frac{1}{2}$ (thỏa mãn đk x ≠ 0)
Với $ \displaystyle x=\frac{1}{2}\Rightarrow y=\frac{1}{3}$ (thỏa mãn đk y ≠ 0)
Vậy hệ phương trình đã cho có 1 nghiệm $ (x;y)=(\frac{1}{2};\frac{1}{3})$