Thời gian làm bài 120 phút (không kể phát đề).
Đề thi:
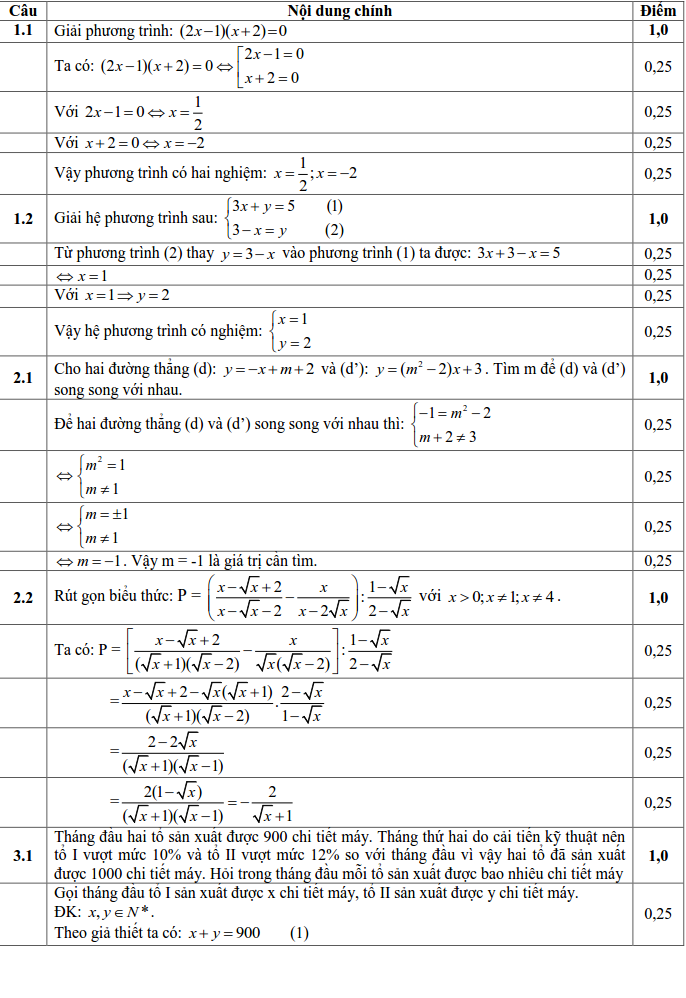
Câu 1 (2,0 điểm) Giải phương trình và hệ phương trình sau:
1) $ (2x-1)(x+2)=0$ 2) $ \left\{ \begin{array}{l}3x+y=5\\3-x=y\end{array} \right.$
Câu 2 (2,0 điểm)
1) Cho hai đường thẳng (d): $ y=-x+m+2$ và (d’): $ \displaystyle y=({{m}^{2}}-2)x+3$. Tìm m để (d) và (d’) song song với nhau.
2) Rút gọn biểu thức: $ P=\left( \frac{x-\sqrt{x}+2}{x-\sqrt{x}-2}-\frac{x}{x-2\sqrt{x}} \right):\frac{1-\sqrt{x}}{2-\sqrt{x}}$ với $ x>0;x\ne 1;x\ne 4$.
Câu 3 (2,0 điểm)
1) Tháng đầu, hai tổ sản xuất được 900 chi tiết máy. Tháng thứ hai, do cải tiến kỹ thuật nên tổ I vượt mức 10% vả tổ II vượt mức 12% so với tháng đầu, vì vậy, hai tổ đã sản xuất được 1000 chi tiết máy. Hỏi trong tháng đầu mỗi tổ sản xuất được bao nhiêu chi tiết máy ?
2) Tìm m để phương trình: $ {{x}^{2}}+5x+3m-1=0$ (x là ẩn, m là tham số) có hai nghiệm x1, x2 thỏa mãn $ x_{1}^{3}-x_{2}^{3}+3{{x}_{1}}{{x}_{2}}=75$.
Câu 4 (3,0 điểm) Cho đường tròn tâm O, bán kính R. Từ một điểm M ở ngoài đường tròn, kẻ hai tiếp tuyến MA và MB với đường tròn (A, B là các tiếp điểm). Qua A, kẻ đường thẳng song song với MO cắt đường tròn tại E (E khác A), đường thẳng ME cắt đường tròn tại F (F khác E), đường thẳng AF cắt MO tại N, H là giao điểm của MO và AB.
1) Chứng minh: Tứ giác MAOB nội tiếp đường tròn.
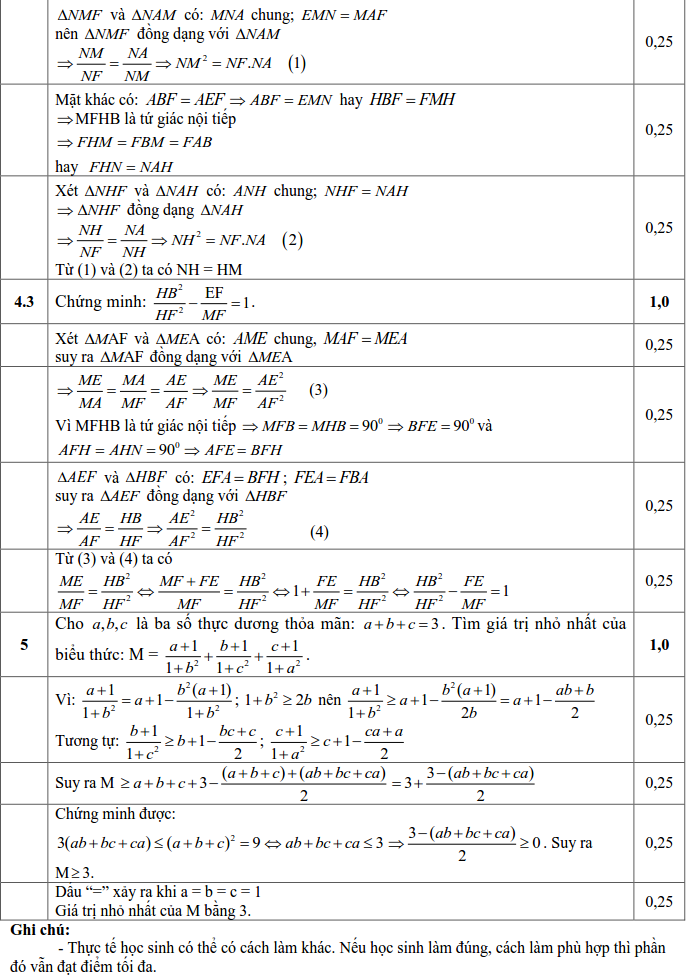
2) Chứng minh: MN2 = NF.NA vả MN = NH.
3) Chứng minh: $ \frac{H{{B}^{2}}}{H{{F}^{2}}}-\frac{EF}{MF}=1$.
Câu 5 (1,0 điểm) Cho x, y, zlà ba số thực dương thỏa mãn: $ x+y+z=3$.Tìm giá trị nhỏ nhất của biểu thức: $ Q=\frac{x+1}{1+{{y}^{2}}}+\frac{y+1}{1+{{z}^{2}}}+\frac{z+1}{1+{{x}^{2}}}$.
Đáp án và biểu điểm: