Giải phương trình bậc hai bằng đồ thị. Vị trí tương đối giữa parabol $y=ax^2$ và đường thẳng y=mx+n

Giải phương trình bậc hai bằng đồ thị

Kiến thức cần nhớ:

1. Giải phương trình bậc hai bằng đồ thị :

Để giải phương trình bậc hai a + bx + c = 0 (tức là a = -bx – c) bằng đồ thị, ta vẽ parabol y = a và đường thắng y = -bx – c trong cùng một hệ trục toạ độ, rồi xác định hoành độ các giao điểm của chúng (nếu có).

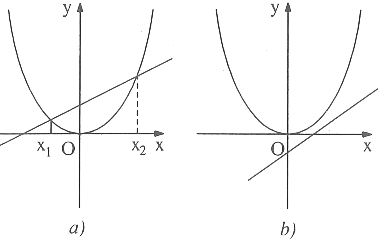
Nếu đường thẳng cắt parabol tại hai điểm (h.a) thì phương trình có hai nghiệm (trường hợp này ứng với Δ > 0).

Nếu đường thẳng không giao với parabol (h.b) thì phương trình vô nghiệm (trường hợp này ứng với Δ < 0).

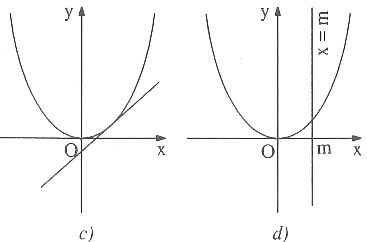
Nếu đường thẳng tiếp xúc với parabol (h.c) thì phương trình có nghiệm kép (trường hợp này ứng với Δ = 0).

     Chú ý:

     Một đường thẳng gọi là tiếp xúc với parabol nếu nó có một điểm chung duy nhất với parabol và parabol nằm về một phía của đường thẳng (h.c). Ở hình d, đường thẳng x = m cũng chỉ có một điểm chung với parabol nhưng ta không gọi là tiếp xúc với parabol.

2. Vị trí tương đối giữa parabol y = a (a ≠ 0) và đường thẳng y = mx + n :

Xét phương trình

a = mx + n tức là ax – mx – n = 0                         (1)

Đường thẳng cắt parabol tại hai điểm phân biệt <=> (1)      có Δ > 0.

Đường thẳng không giao với parabol <=> (1) có Δ < 0.

Đường thẳng tiếp xúc với parabol <=> (1) có Δ = 0.

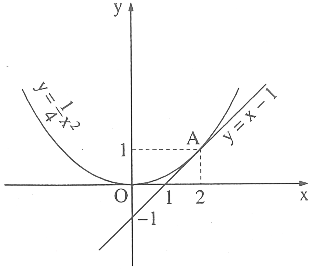
Ví dụ 37. Cho parabol y = a tiếp xúc với đường thẳng y = x – 1,

a)   Xác định hệ số a ;

b)  Tìm toạ độ tiếp điểm của đường thẳng và parabol;

c)   Vẽ parabol và đường thẳng nói trên cùng một hê trục toạ độ.

Giải

a)   Điều kiện để parabol y = a tiếp xúc với đường thẳng y = x – 1 là phương trình

a = x – 1                                                (1)

có nghiệm kép.

Ví dụ 38. Cho parabol

a) Chứng minh rằng đường thẳng y = 2x – 2 () tiếp xúc với parabol. Tìm toạ độ của tiếp điểm.

b) Cho biết điều kiện để hai đường thẳng y = ax + b và y = a’x + b’ vuông góc với nhau là aa’ = -1. Xác định tiếp tuyến  của parabol sao cho ⊥ .

c) Tìm toạ độ giao điểm của hai đường thẳng và .

d) Chứng minh rằng giao điểm các tiếp tuyến của parabol mà vuông góc với nhau nằm trên đường thẳng y = -1/2.

Giải:

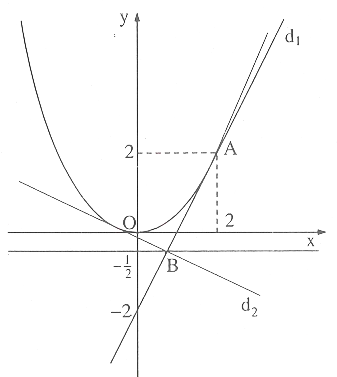
d)  Xét hai đường thẳng y = ax b và y = a’x + b’ vuông góc với nhau (aa’ = -1). Trước hết ta tìm toạ độ của giao điểm hai đường thẳng đó.

BÀI TẬP

212. Cho parabol y = . Xác định hệ số n để đường thẳng y = 2x + n tiếp xúc với parabol. Tìm toạ độ của tiếp điểm.

213. Cho parabol y = và đường thẳng y = mx + n.

Xác định các hệ số m và n để đường thẳng đi qua điểm A(-l ; 0) và tiếp xúc với parabol. Tìm toạ độ của tiếp điểm.

214. Cho parabol y = . Lập phương trình đường thẳng đi qua điểm A(-l ; -2) và tiếp xúc với parabol. Tìm toạ độ của tiếp điểm.

215. Cho parabol y =  và đường thẳng y = x n.

a) Với giá trị nào của n thì đường thẳng cắt parabol tại hai điểm phân biệt ?

b) Xác định toạ độ giao điểm của parabol và đường thẳng nếu n = 2.

216. Vẽ đồ thị của hàm số y =   1 | – 1|.

217. Giải các phương trình sau bằng phương pháp đồ thị :

a) 2 – 1 = |x – 2| ;                                           b) – 4|x – 1| 4 = 0

218. Cho hàm số:    y = a

a) Xác định a và vẽ đồ thị của hàm số biết rằng đồ thị của hàm số đi qua điểm (2 ; 2).

b) Gọi A, B là các giao điểm của parabol nói ở câu a) với đường thẳng y = x 3. Tìm toạ độ của A, B và tính diện tích tam giác OAB.

219. Cho parabol y = và đường thẳng y = 2x + n.

a)  Biện luận theo n về số giao điểm của parabol với đường thẳng.

b) Vẽ parabol và đường thẳng trong trường hợp đường thẳng tiếp xúc với parabol.

220. Cho đường thẳng

y = 2x – 1 (d).

a)  Xác định a sao cho parabol y = a tiếp xúc với d. Tìm toạ độ của tiếp điểm.

b) Xác định m và n sao cho đường thẳng y = mx n đi qua điểm A(3 ; 2) và vuông góc với d (hai đường thẳng vuông góc với nhau nếu tích hai hệ số góc bằng -1).

221. Cho parabol                     y =

a)  Chứng minh rằng đường thẳng y = 2x + 1 () tiếp xúc với parabol. Tìm toạ độ của tiếp điểm.

b) Cho biết hai đường thẳng vuông góc với nhau nếu tích hai hệ số góc bằng -1. Xác định tiếp tuyến  với parabol nói trên sao cho ⊥ .

c)  Tìm toạ độ giao điểm của hai đường thẳng và .

d) Chứng minh rằng giao điểm của các tiếp tuyến với parabol mà vuông góc với nhau nằm trên một đường thẳng song song với trục hoành.

222. Bằng đồ thị, giải các bất phương trình sau :

a)  < 4 ;                               b)  – x – 2 < 0.