Kiến thức cần nhớ
Hàm số $y = ax^2$, (a ≠ 0)
1. Hàm số xác định với mọi giá trị X thuộc R.
2. Tính chất biến thiện :
– Nếu a > 0 thì hàm số nghịch biến khi x < 0, đồng biến khi x > 0.
– Nếu a < 0 thì hàm số đồng biến khi x < 0, nghịch biến khi x > 0.
3. Đồ thị của hàm số là đường parabol với các đặc điểm :
– Đỉnh 0(0 ; 0).
– Trục đối xứng Oy.
– Nếu a > 0 thì đồ thị nằm phía trên trục hoành, nhận gốc toạ độ làm điểm thấp nhất.
– Nếu a < 0 thì đồ thị nằm phía dưới trực hoành, nhận gốc toạ độ làm điểm cao nhất.
Ví dụ 20.
A) Hãy xác định hệ số a của hàm số y = a
b) Vẽ đồ thị của hàm số đó.
c) Tìm các điểm thuộc parabol nói trên có tung độ bằng 4,5.
d) Tìm m sao cho điểm C(-2 ; m) thuộc parabol.
e) Có bao nhiêu điểm thuộc parabol mà cách đều hai trục toạ độ ?
Giải(h.4)
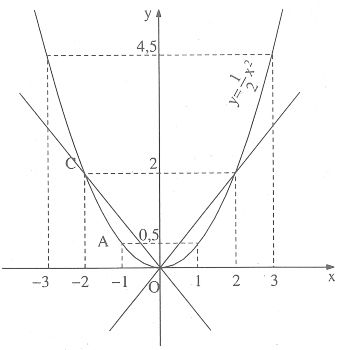
Hình 4
Có ba điểm thuộc parabol và cách đều hai trục toạ độ là : (0 ; 0), (2 ; 2), (-2 ; 2).
BÀI TẬP
129.
Người ta chứng minh được rằng nếu thả một vật rơi tự do thì sau t giây vật rơi được quãng đường s = 
trường và có giá trị khoảng 9,8 (bỏ qua sức cản của không khí). Ta lấy g ≈ 10.
a) Lập công thức biểu thị quãng đường s (tính bằng mét) của vật đi được sau t giây.
b) Vẽ đồ thị của hàm số (trong đó để thể hiện hướng di chuyển của vật từ trên xuống dưới, chọn hướng của tia Os từ trên xuống dưới).
c) Tính thời gian để một hòn đá rơi tự do từ miệng xuống đáy một giếng khoan có độ sâu 60m.
130.
Cho hàm số
y = (2m – 1)
a) Xác định giá trị của m biết rằng đồ thị của hàm số đi qua điểm (3 ; -3). Vẽ đồ thị của hàm số.
b) Một đường thẳng song song với trục hoành cắt trục tung tại điểm -4 và cắt parabol nói ở câu a tại các điểm A, B. Tính diện tích tam giác AOB.
131.
Vẽ đồ thị của các hàm số:
132.
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số :
