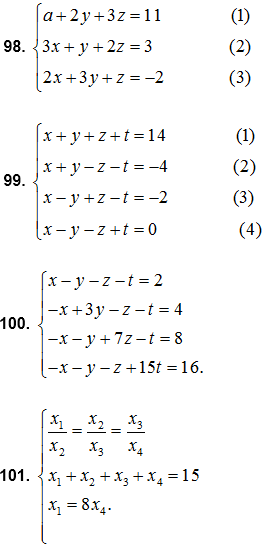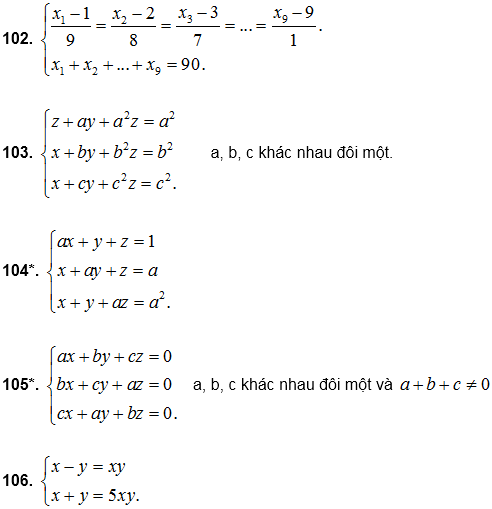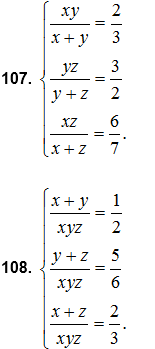Ví dụ 17. Cho hệ phương trình
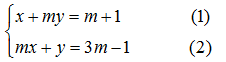
a) Không giải hệ phương trình, cho biết với giá trị nào của m thì hệ phương trình có nghiệm duy nhất.
b) Giải và biện luận hệ phương trình trên.
Giải
a) Hệ phương trình có nghiệm duy nhất khi và chỉ khi
ab’ – a’b ≠ 0 <=> 1.1 – m.m ≠ 0 <=> 1 – ≠ 0 <=> m ≠ ± 1.
Với m ≠ ± 1 thì hệ phương trình có nghiệm duy nhất.
b) Rút x từ (1) ta được x = m 1 – my.
Thay biểu thức của x vào (2) :
m(m 1 – my) y = 3m – 1 <=> m –
y y = 3m – 1
<=> y – y =
2m – 1 <=> (1 –
)y =
.
Nếu m ≠ ± 1 thì
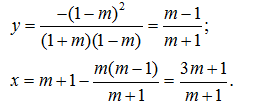
Nếu m = 1 thì hệ phương trình đã cho trở thành

Nếu m = -1 thì hệ đã cho trở thành
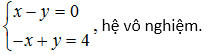
Kết luận :
– Nếu m ≠ ± 1, hệ phương trình đã cho có nghiệm duy nhất
![]()
– Nếu m = 1, hệ phương trình đã cho có vô số nghiệm ; x bất kì, y = 2 – x.
– Nếu m = -1, hệ phương trình đã cho vô nghiệm.
BÀI TẬP
80. Giải các hệ phương trình:
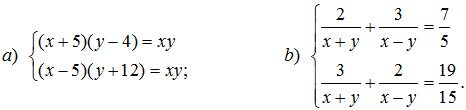
81. Cho hệ phương trình:
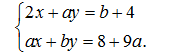
Xác định các hệ số a và b để hệ phương trình có nghiệm x = 3, y = -2.
82. Cho hai đường thẳng:
2x – y = -6 và x y = 3.
a) Tìm toạ độ giao điểm M của hai đường thẳng.
b) Gọi giao điểm của hai đường thẳng trên với trục hoành theo thứ tự là A và B. Tính diện tích tam giác MAB.
83. Lập phương trình đường thẳng đi qua giao điểm của hai đường thẳng 2x – 3y = 8 ; 5x 4y = -3 và song song với đường thẳng y = 2x – 1.
84. Xác định các hệ số a và b để đường thẳng y = ax b đi qua hai điểm M(3 ; 5) và N(-1 ; -7). Tìm toạ độ giao điểm của đường thẳng vừa tìm được với các trục toạ độ.
85. Xác định giá trị của a để các đường thẳng sau đồng quy :
y = ax, y = 3x – 10 và 2x 3y = -8.
86. Cho ba điểm A(3 ; 5), B(-1 ; -7), C(1 ; -1). Chứng minh rằng ba điểm A,
B, C thẳng hàng.
87. Cho bốn điểm A(-1 ; 1), B(3 ; 2), C(2 ; -1), D(-2 ; -2).
a) Lập phương trình các đường thẳng AB, BC, CD, DA.
b) Chứng minh rằng tứ giác ABCD là hình bình hành.
88. Tìm giá trị của a để hệ phương trình sau có nghiệm dương :
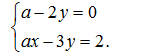
89.
Tìm giá trị của m để giao điểm của hai đường thẳng mx – y = 2, 3x my = 5 nằm trong góc vuông phần tư IV. (Các góc vuông phần tư I, II, III, IV được kí hiệu như trên hình 3).
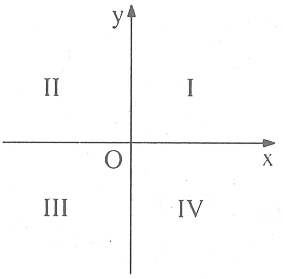
Hình 3
90. Tìm giá trị nguyên của m để giao điểm của các đường thẳng mx – 2y = 3 và 3x my = 4 nằm trong góc vuông phần tư IV.
91. Giải và biện luận hệ phương trình
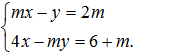
92. Tìm giá trị của m để hệ phương trình
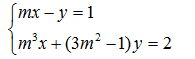
vô nghiệm, vô số nghiệm.
93.
Tìm giá trị của m để các đường thẳng
(d1) : mx (m – 1)y = 3m 4
(d2) : 2mx (m 1)y = m- 4
a) Cắt nhau ; b) Song song ; c) Trùng nhau.
94. Giải hệ phương trình:
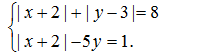
95.
Tìm nghiệm nguyên dương của các phương trình :
a) (3x – y)(5x 3y) =11; b) (x 2y)(3x 4y) = 96.
96*. Viết số 100 thành tổng các số nguyên dương liên tiếp.
97*. Viết số 117 thành tổng các số nguyên dương lẻ liên tiếp.
Giải các hệ phương trình (từ bài 98 đến 108) :