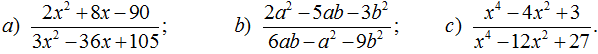Kiến thức cần nhớ:
Ví dụ 23. Cho phương trình
a) Chứng minh rằng phương trình luôn có nghiệm với mọi k.
b) Tìm k để phương trình có hai nghiệm cùng dấu. Khi đó hai nghiệm mang dấu gì?
c) Tìm k để phương trình có tổng hai nghiệm bằng 6. Tìm hai nghiệm đó.
Giải
a) Phương trình đã cho là phương trình bậc hai.
Ví dụ 24. Cho phương trình
Ví dụ 25.
Gọi m và n là các nghiệm của phương trình
Hiển nhiên m, n đều khác -1 và -1 không thoản mãn phương trình (1).
Ta có:
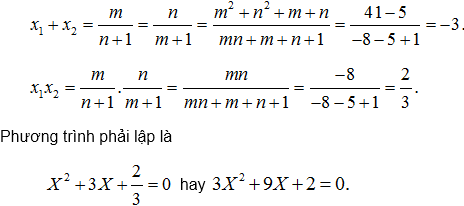
Ví dụ 26.
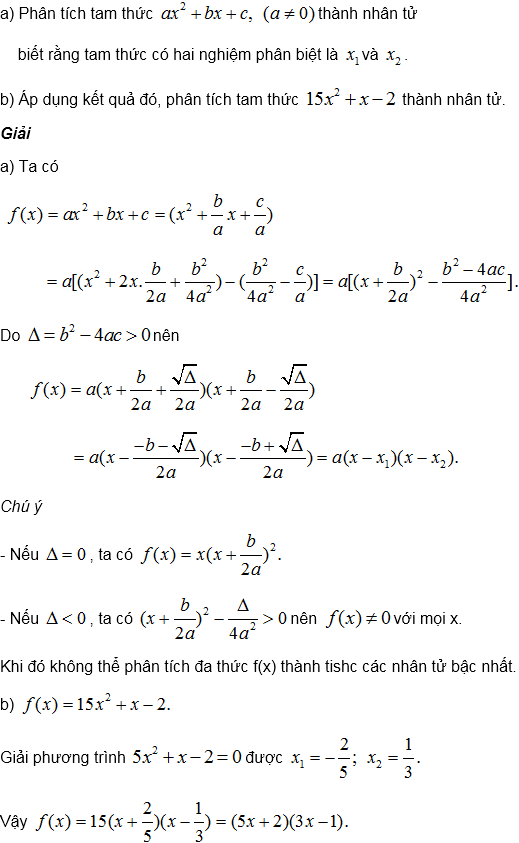
BÀI TẬP
146. Tìm nghiệm của các phương trình sau:
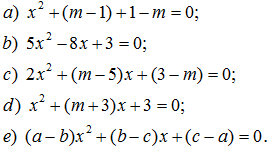
147. Xác định m và tìm nghiệm còn lại biết rằng:
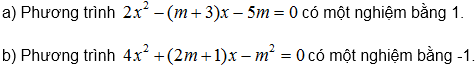
148. Cho phương trình:
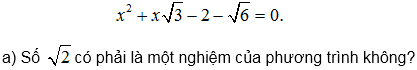
b) Tìm nghiệm còn lại.
149. Không giải phương trình, xác định dấu hiệu của các nghiệm (nếu có):
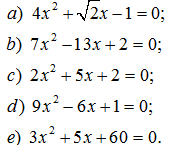
150. Xác định số k để các phương trình sau có nghiệm phân biệt cùng dấu:
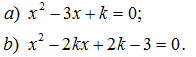
151. Tìm giá trị của m để phương trình sau có hai nghiệm phân biệt cùng dấu.
Khi đó hai nghiệm mang dấu gì?
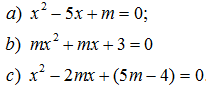
152. Xác định số k để các phương trình sau có hai nghiệm trái dấu:
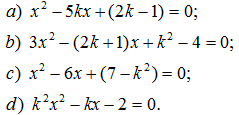
153. Cho phương trình 
a) Tổng và tích các nghiệm;
b) Tổng các nghịch đảo và các nghiệm;
c) Tổng các bình phương của các nghiệm;
d) Bình phương của hiệu các nghiệm;
e) Hiệu các nghiệm.
154. Cũng hỏi như bài 153 đối với phương trình 3
155. Xác định số k để các phương trình sau có hai nghiệm mà hiệu của chúng bằng 1.
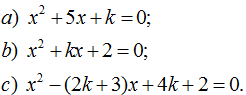
a) Hai số đối nhau ; b) Hai số nghịch đảo nhau.
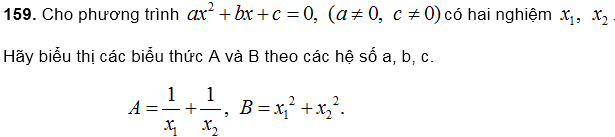
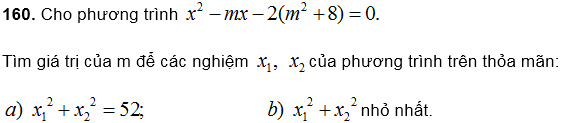
161. Cho phương trình:
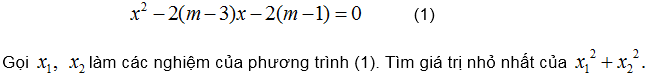
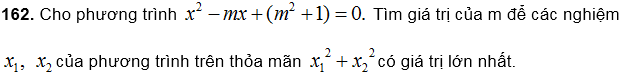
163. Tìm giá tị của m để phương trình sau có hai nghiệm phân biệt nhỏ hơn 1.
164.Cho phương trình:
a) Tìm giá trị của m để phương trình có một nghiệm nhỏ hơn 1, một nghiệm lơn hơn 1.
b) Tìm giá trị của m để phương trình có hai nghiệm nhỏ hơn 2.
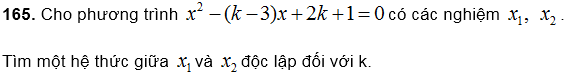
166. Tìm hai sốm và n biết tổng S và tishc P của chúng
167. Lập phương trình bậc hai có các nghiệm bằng:
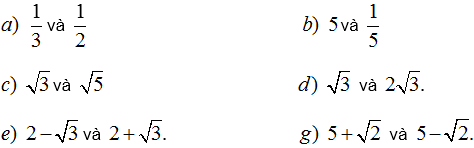
168. Chứng minh rằng tồn tại một phương trình bậc hai có các hệ số là số hữu tỉ và có một trong các nghiệm bằng:
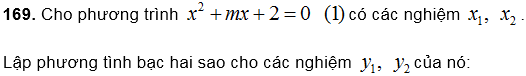
a) Gấp hai lần các nghiệm của phương trình (1).
b) Là số đối của các nghiệm của phương trình (1).
170. Lập phương trình bậc hai có các nghiệm là nghịch đảo của các nghiệm của phương trình:
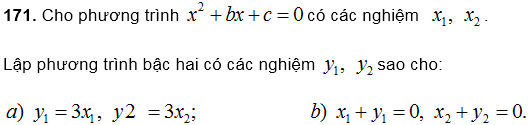
172. Phân tích các tam thức sau thành nhân tử:
173. Rút gọn các phân thức:
