Bài 1: Hai đường thẳng AB và CD cắt nhau tại E tạo thành bốn góc không kể góc bẹt. Biết tổng của ba góc trong bốn góc này bằng $ {{250}^{0}}$, tính số đo của bốn góc đó.
Bài 2:
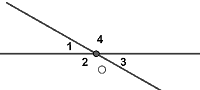
Cho hình vẽ, tính các góc $ {{O}_{1}},\,\,{{O}_{2}},\,\,{{O}_{3}},\,\,{{O}_{4}}$, nếu:
a) $ \widehat{{{O}_{1}}}+\widehat{{{O}_{3}}}={{140}^{0}}$
b) $ \widehat{{{O}_{1}}}+\widehat{{{O}_{3}}}=\widehat{{{O}_{2}}}+\widehat{{{O}_{4}}}$
c) $ \displaystyle \widehat{{{O}_{2}}}-\widehat{{{O}_{1}}}={{10}^{0}}$
Bài 3:
Cho 3 đường thẳng phân biệt xx’, yy’, zz’ cắt nhau tại O. Hình tạo thành có:
a) Bao nhiêu tia chung gốc?
b) Bao nhiêu góc tạo bởi hai tia chung gốc?
c) Bao nhiêu góc bẹt?
d) Bao nhiêu cặp góc đối đỉnh?
Bài 4:
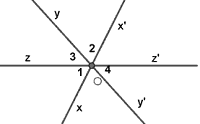
Cho hình vẽ bên:
a) Góc $ {{O}_{1}}$ và góc $ {{O}_{2}}$ có phải là hai góc đối đỉnh không? Vì sao?
b) Tính tổng $ \widehat{{{O}_{1}}}+\widehat{{{O}_{2}}}+\widehat{{{O}_{4}}}$ .
Bài 5:
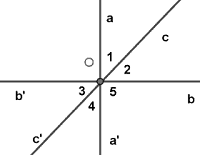
Trên hình vẽ bên, cho $ \widehat{{{O}_{3}}}={{90}^{0}}$.
Tia OC là phân giác của $ \widehat{aOb}$.
Tính $ \displaystyle \widehat{{{O}_{1}}},\,\widehat{\,{{O}_{2}}},\,\widehat{\,{{O}_{3}}},\widehat{\,{{O}_{4}}}$
Bài 6: Cho hai góc xOy và yOx’ là hai góc kề bù, $ \widehat{xOy}={{60}^{0}}$, Ot là tia phân giác của góc xOy. Trên nửa mặt phẳng chứa tia Oy bờ Ox, kẻ tia Om vuông góc với Ox.
a) Tính góc tOm
b) Chứng minh Oy là tia phân giác của góc mOt.
Bài 7: Cho $ \widehat{mOn}={{140}^{0}}$, vẽ các tia OP và OQ nằm giữa hai tia OM và ON sao cho: $ OP\bot OM;\,\,\,OQ\bot ON$.
a) So sánh $ \widehat{MOQ}$ và $ \widehat{NOP}$
b) Tính $ \widehat{POQ}$
Bài 8: Cho góc vuông AOB, hai tia OC, OD ở trong góc đó sao cho $ \widehat{AOC}=\widehat{BOD}={{60}^{0}}$. Trên nửa mặt phẳng bờ OA chứa tia OB, vẽ tia OE sao cho tia OB là phân giác của góc DOE.
a) Hai tia OC, OD là phân giác của những góc nào?
b) Chứng minh OC vuông góc với OE.
Bài 9: Cho hình vẽ bên dưới, hãy chỉ ra các cặp góc có cạnh tương ứng vuông góc