
Kiến thức cần nhớ:
1. Nếu đại lượng y phụ thuộc vào đại lượng thay đổi X sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị số tương ứng của y thì y được gọi là hàm số của x, x được gọi là biến số.
Hàm số có thể được cho bằng bảng, cho bằng công thức,…
2. Cho hàm số y = f(x) xác định trên khoảng (a ; b).
Xét hai giá trị bất kì ,
thuộc khoảng đó sao cho
<
.
– Nếu f() < f(
) thì hàm số f đồng biến trên khoảng (a ; b).
– Nếu f() > f(
) thì hàm số f nghịch biến trên khoảng (a ; b).
3. Đồ thị của hàm số y = f(x) là tập hợp các điểm biểu diễn cặp số (x ; y) trên mặt phẳng toạ độ.
Ví dụ 12. Cho các hàm số :
f(x) = 2x – 1, g(x) = 3 – 2.
a) Tính f(), g(4);
b) Tìm số a sao cho f(a) = g(a) ;
c) Chứng minh rằng hàm số y = g(x) đồng biến với x ≥ 0.
Giải
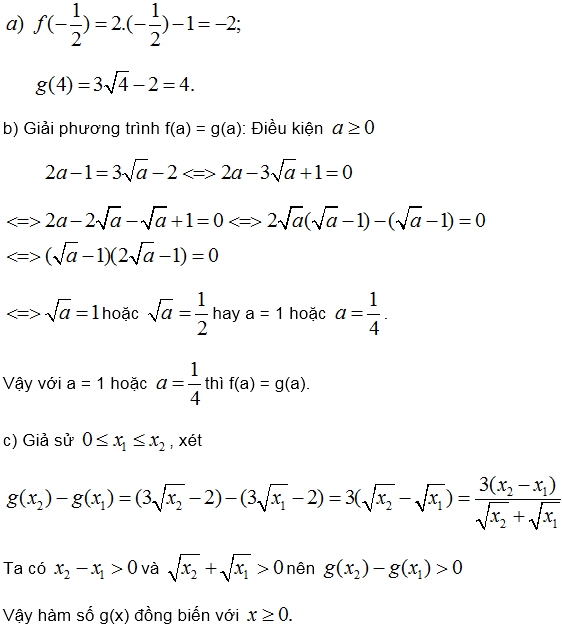
BÀI TẬP
59. Cho các hàm số : f(x) = 6 + 1 và g(x) = 5x.
a) Tìm a sao cho f(a) = g(a).
b) Chứng minh rằng f(x) = f(-x), g(x) = -g(-x).
60. Chứng minh rằng hàm số y = ax + b với a > 0 đồng biến trên tập hợp số thực R.
61. Cho hàm số y = 2 – 8x + 1. Chứng minh rằng hàm số nghịch biến khi x < 2, đồng biến khi x > 2.